(本小题满分13分)

已知数列满足，且对任意，都有．

(Ⅰ）求证：数列为等差数列；

(Ⅱ）试问数列中是否仍是中的项？如果是，请指出是数列的第几项；如果不是，请说明理由．

（Ⅲ）令   证明：对任意.

（本小题满分13分）

解: （Ⅰ），即，          ……1分

所以，                                              ……. 2分

所以数列是以为首项，公差为的等差数列．                     ……3分

（II）由（Ⅰ）可得数列的通项公式为，所以．…… 4分

                          …….5分

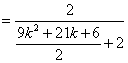
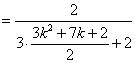．                              …… 7分

因为，                           …… 8分

当时，一定是正整数，所以是正整数．

(也可以从k的奇偶性来分析)                                       

所以是数列中的项，是第项．                 …… 9分

(Ⅲ)证明：由（2）知：， …..10分

下面用数学归纳法证明：对任意。

(1)当时，显然，不等式成立.                                 …..11分

(2)假设当

当

….12分

即有：也成立。

综合(i)(ii)知：对任意               ……13分

关闭