【题目】已知函数f(x)= ![]() .
.
(1)判断函数f(x)的奇偶性;
(2)判断并证明f(x)的单调性;
(3)求关于x的不等式f(2x﹣1)+f(x+3)>0的解集.
参考答案:
【答案】
(1)解:函数的定义域为R,
因为f(x)= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
所以f(﹣x)= ![]() =
= ![]() ,
,
则f(x)+f(﹣x)= ![]() +
+ ![]() =0,
=0,
所以f(x)是奇函数
(2)解:函数f(x)在(﹣∞,+∞)上为减函数,
由(1)得,f(x)= ![]() ,
,
设任意x1,x2∈R,且x1<x2,
f(x1)﹣f(x2)= ![]() ﹣(
﹣( ![]() )
)
= ![]() =
= ![]() ,
,
∵x1<x2,∴ ![]() ,
,
∴f(x1)﹣f(x2)>0,即f(x1)>f(x2),
∴函数f(x)在(﹣∞,+∞)上为减函数
(3)解:由(1)得f(x)是奇函数,
∴不等式f(2x﹣1)+f(x+3)>0等价于f(2x﹣1)>f(﹣x﹣3),
∵函数f(x)在(﹣∞,+∞)上为减函数,
∴2x﹣1<﹣x﹣3,解得x< ![]() ,
,
∴不等式的解集是(﹣∞, ![]() )
)
【解析】(1)求出函数的定义域,利用指数的运算法则化简f(x)、f(﹣x),由函数奇偶性的定义判断出奇偶性;(2)利用指数函数的单调性判断出f(x)的单调性,利用定义法证明函数单调性步骤:取值、作差、变形、定号、下结论进行证明;(3)由奇函数的性质等价转化不等式f(2x﹣1)+f(x+3)>0,由单调性列出不等式求出解集.
【考点精析】本题主要考查了奇偶性与单调性的综合的相关知识点,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,(1)已知a=
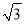 ,b=
,b=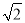 ,B=45°,求A、C、c;
,B=45°,求A、C、c;(2)已知sin A∶sin B∶sin C=(
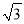 +1)∶(
+1)∶(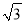 -1)∶
-1)∶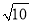 ,求最大角.
,求最大角. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
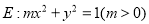 .
.(1)若椭圆
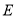 的右焦点坐标为
的右焦点坐标为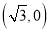 ,求
,求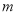 的值;
的值;(2)由椭圆
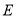 上不同三点构成三角形称为椭圆的内接三角形.若以
上不同三点构成三角形称为椭圆的内接三角形.若以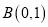 为直角顶点的椭圆
为直角顶点的椭圆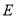 的内接等腰直角三角形恰有三个,求
的内接等腰直角三角形恰有三个,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|x2﹣3x+2=0},B={x|x2+2(a+1)x+(a2﹣5)=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两个容器,甲容器容量为
 ,装满纯酒精,乙容器容量为
,装满纯酒精,乙容器容量为 ,其中装有体积为
,其中装有体积为 的水(
的水(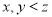 :单位:
:单位:  ).现将甲容器中的液体倒人乙容器中,直至甲容器中液体倒完或乙容器盛满,搅拌使乙容器中两种液体充分混合,再将乙容器中的液体倒人甲容器中直至倒满,搅拌使甲容器中液体充分混合,如此称为一次操作,假设操作过程中溶液体积变化忽略不计.设经过
).现将甲容器中的液体倒人乙容器中,直至甲容器中液体倒完或乙容器盛满,搅拌使乙容器中两种液体充分混合,再将乙容器中的液体倒人甲容器中直至倒满,搅拌使甲容器中液体充分混合,如此称为一次操作,假设操作过程中溶液体积变化忽略不计.设经过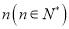 次操作之后,乙容器中含有纯酒精
次操作之后,乙容器中含有纯酒精 (单位:
(单位:  ),下列关于数列
),下列关于数列 的说法正确的是( )
的说法正确的是( )A. 当
 时,数列
时,数列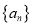 有最大值
有最大值
B. 设
 ,则数列
,则数列 为递减数列
为递减数列C. 对任意的
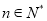 ,始终有
,始终有
D. 对任意的
 ,都有
,都有
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合
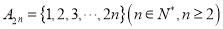 .如果对于
.如果对于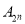 的每一个含有
的每一个含有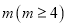 个元素的子集
个元素的子集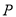 ,
, 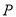 中必有4个元素的和等于
中必有4个元素的和等于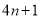 ,称正整数
,称正整数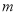 为集合
为集合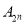 的一个“相关数”.
的一个“相关数”.(Ⅰ)当
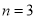 时,判断5和6是否为集合
时,判断5和6是否为集合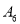 的“相关数”,说明理由;
的“相关数”,说明理由;(Ⅱ)若
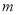 为集合
为集合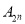 的“相关数”,证明:
的“相关数”,证明: 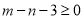 ;
;(Ⅲ)给定正整数
 .求集合
.求集合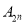 的“相关数”
的“相关数” 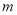 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,有下列说法:
①若f(a)f(b)>0,则函数y=f(x)在区间(a,b)上没有零点;
②若f(a)f(b)>0,则函数y=f(x)在区间(a,b)上可能有零点;
③若f(a)f(b)<0,则函数y=f(x)在区间(a,b)上没有零点;
④若f(a)f(b)<0,则函数y=f(x)在区间(a,b)上至少有一个零点;
其中正确说法的序号是(把所有正确说法的序号都填上).
相关试题

