【题目】(导学号：05856333)

已知椭圆C： (a>b>0)的离心率为，其右焦点为F(c,0)，第一象限的点A在椭圆C上，且AF⊥x轴．

(Ⅰ)若椭圆C过点(1，－ )，求椭圆C的标准方程；

(Ⅱ)已知直线l：y＝x－c与椭圆C交于M，N两点，且B(4c，yB)为直线l上的点，证明：直线AM，AB，AN的斜率满足kAB＝.

【答案】(1) (2)见解析

【解析】试题分析：（1）运用椭圆的离心率公式和点满足椭圆方程，结合a，b，c的关系，解方程可得a，b，进而得到椭圆方程；

（2）由离心率公式可得椭圆C的方程为3x2+4y2=12c2，将直线方程代入椭圆方程，运用韦达定理，再由直线的斜率公式化简整理，即可得证．

试题解析：

(Ⅰ)依题意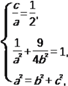，解得a＝2，b＝，c＝1，

故椭圆C的标准方程为＋＝1.

(Ⅱ)因为e＝，故a＝2c，b＝c，

∴椭圆C：3x2＋4y2＝12c2，

将直线l的方程为y＝x－c代入椭圆方程并整理，得7x2－8cx－8c2＝0，

设M(x1，y1)，N(x2，y2)，则有x1＋x2＝，x1·x2＝－，可知B的坐标为(4c,3c)，

A的坐标为(c， c)，故kAM＋kAN＝＋＝，

将x1＋x2＝，x1·x2＝－代入可得，kAM＋kAN＝1，kAB＝＝，

∴kAB＝.

关闭