Question

【题目】如图所示，是边长，的矩形硬纸片，在硬纸片的四角切去边长相等的小正方形后，再沿虚线折起，做成一个无盖的长方体盒子，、是上被切去的小正方形的两个顶点，设.

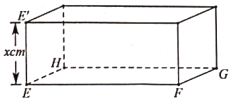
（1）将长方体盒子体积表示成的函数关系式，并求其定义域；

（2）当为何值时，此长方体盒子体积最大？并求出最大体积.

Answer 1

【答案】（1），；（2）当时长方体盒子体积最大，此时最大体积为.

【解析】

（1）分别由题意用x表示长方体的长宽高，代入长方体的体积公式即可表示该函数关系，再由实际长方体的长宽高都应大于零构建不等式组，即可求得定义域.

（2）利用导数分析体积在定义域范围内的单调性，进而求函数的最大值.

长方体盒子长，宽，高.

（1）长方体盒子体积，

由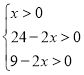得，故定义域为.

（2）由（1）可知长方体盒子体积

则，在内令，解得，故体积V在该区间单调递增；

令，解得，故体积V在该区间单调递减；

∴在取得极大值也是最大值.此时.

故当时长方体盒子体积最大，此时最大体积为.