【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为:
的参数方程为: (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的面积.
的面积.
参考答案:
【答案】(1)直线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)直线![]() 的参数方程为:
的参数方程为: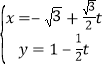 (
(![]() 为参数),消去t即可;曲线
为参数),消去t即可;曲线![]() 的极坐标方程为
的极坐标方程为![]() ,利用直角坐标与极坐标之间的互化公式即可;
,利用直角坐标与极坐标之间的互化公式即可;
(2)转换成直角坐标去进行求解.
详解:(1)因为直线![]() 的参数方程为
的参数方程为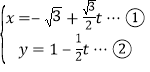 ,
,![]() 得
得![]() ,
,
故直线![]() 的普通方程为
的普通方程为![]() ,
,
又曲线![]() 的极坐标方程为
的极坐标方程为![]() ,即
,即![]() ,
,
因为![]() ,
,![]() ,∴
,∴![]() ,即
,即![]() ,
,
故曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)因为点![]() 的极坐标为
的极坐标为![]() ,∴点
,∴点![]() 的直角坐标为
的直角坐标为![]() ,∴点
,∴点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
将![]() ,代入
,代入![]() 中得
中得![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
∴![]() 的面积
的面积![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=
 ,E,F分别是BC,A1C的中点.
,E,F分别是BC,A1C的中点. 
(1)求异面直线EF,AD所成角的余弦值;
(2)点M在线段A1D上, =λ.若CM∥平面AEF,求实数λ的值.
=λ.若CM∥平面AEF,求实数λ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】把圆分成
 个扇形,设用4种颜色给这些扇形染色,每个扇形恰染一种颜色,并且要求相邻扇形的颜色互不相同,设共有
个扇形,设用4种颜色给这些扇形染色,每个扇形恰染一种颜色,并且要求相邻扇形的颜色互不相同,设共有 种方法.
种方法.(1)写出
 ,
, 的值;
的值;(2)猜想

 ,并用数学归纳法证明。
,并用数学归纳法证明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了巩固全国文明城市创建成果,今年吉安市开展了拆除违章搭建铁皮棚专项整治行为.为了了解市民对此项工作的“支持”与“反对”态度,随机从存在违章搭建的户主中抽取了男性、女性共
 名进行调查,调查结果如下:
名进行调查,调查结果如下:支持
反对
合计
男性



女性



合计



(1)根据以上数据,判断是否有
 的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;(2)现从参与调查的女户主中按此项工作的“支持”与“反对”态度用分层抽样的方法抽取
 人,从抽取的
人,从抽取的 人中再随机地抽取
人中再随机地抽取 人赠送小礼品,记这
人赠送小礼品,记这 人中持“支持”态度的有
人中持“支持”态度的有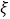 人,求
人,求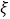 的分布列与数学期望.
的分布列与数学期望.参考公式:
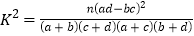 ,其中
,其中 .
.参考数据:








-
科目: 来源: 题型:
查看答案和解析>>【题目】现有
 (n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:
(n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵: 
设Mk是第k行中的最大数,其中1≤k≤n,k∈N*.记M1<M2<…<Mn的概率为pn .
(1)求p2的值;
(2)证明:pn> .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率等于
 .现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校艺术节对同一类的
 ,
, ,
, ,
, 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“是
 或
或 作品获得一等奖”;
作品获得一等奖”;乙说:“
 作品获得一等奖”;
作品获得一等奖”;丙说:“
 ,
, 两项作品未获得一等奖”;
两项作品未获得一等奖”;丁说:“是
 作品获得一等奖”.
作品获得一等奖”.若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
相关试题

