搜索
(本小题满分12分)已知等差数列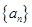
满足：
，
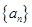，的前n项和为
．
（Ⅰ）求通项公式
及前n项和；
（Ⅱ）令
=
(n
N*)，求数列
的前n项和
．
【答案】
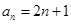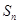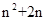（Ⅰ）
； 
=
；（Ⅱ）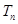
=
。
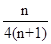【解析】
试题分析：（1）结合已知中的等差数列的项的关系式，联立方程组得到其通项公式和前n项和。
（2）在第一问的基础上，得到bn的通项公式，进而分析运用裂项法得到。
解：（Ⅰ）设等差数列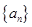
的公差为d，由已知可得
，
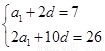解得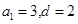
，……………2分，
所以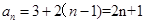
；………4分
=
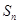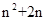=………6分
（Ⅱ）由（Ⅰ）知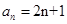
，
所以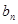
=
=
=
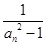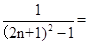
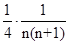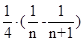……9分
所以=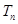
=
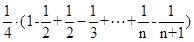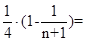
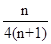
即数列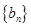
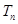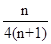的前n项和= ……12分
考点：本试题主要考查了等差数列的通项公式以及前n项和的求解运用。
点评：解决该试题的关键是能得到等差数列的通项公式，然后求解新数列的通项公式，利用裂项的思想来得到求和。易错点就是裂项的准确表示。
