
【题目】如图,在四楼锥![]() 中,
中,![]() 面
面![]() ,
,![]() ,
,![]() .
.
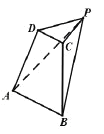
(1)求![]() 的长.
的长.
(2)求直线![]() 与面
与面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)可证![]() 平面
平面![]() ,从而得到
,从而得到![]() 后可计算
后可计算![]() 的长.
的长.
(2)在直角梯形中可计算出![]() ,再利用等积法求出
,再利用等积法求出![]() 到平面
到平面![]() 的距离(可转化
的距离(可转化![]() 到平面
到平面![]() 的距离),从而可得线面角的正弦值.
的距离),从而可得线面角的正弦值.
解:(1)![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,
![]() 平面ABCD,
平面ABCD,
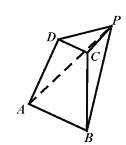
![]() 是直角三角形,
是直角三角形,
由已知![]() ,
,![]() .
.
(2)解法1:
![]() 平面
平面![]() ,
,![]() ,
,
如图,在直角梯形![]() 中,过
中,过![]() 作
作![]() ,交
,交![]() 于
于![]() .
.
故![]() ,所以
,所以![]() .
.

设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
则![]() .
.
![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 到平面
到平面![]() 的距离也为
的距离也为![]() .
.
在三棱锥![]() 中,
中,![]() ,
,
![]() 平面ABCD,
平面ABCD,![]() .
.
又![]() ,
,
![]() ,
,
![]() ,
,![]()
即直线![]() 与面
与面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
解法2:由(1)知![]() 平面ABCD,过
平面ABCD,过![]() 作
作![]() 于
于![]() ,则
,则![]() ,
,
如图以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.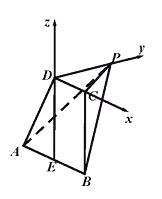
则![]() ,
,
则![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则由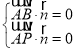 ,得
,得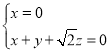
令![]() .可得
.可得![]() .
.
设直线![]() 与面
与面![]() 所成角为
所成角为![]() .
.
则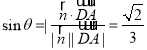 ,即直线
,即直线![]() 与面
与面![]() 所成角的正弦值为
所成角的正弦值为![]()


科目:高中数学 来源: 题型:
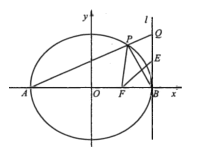
【题目】在平面直角坐标系xOy中,己知椭圆C:![]() 的左、右顶点为A,B,右焦点为F.过点A且斜率为k(
的左、右顶点为A,B,右焦点为F.过点A且斜率为k(![]() )的直线交椭圆C于另一点P.
)的直线交椭圆C于另一点P.
(1)求椭圆C的离心率;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)设直线l:![]() ,延长AP交直线l于点Q,线段BO的中点为E,求证:点B关于直线EF的对称点在直线PF上。
,延长AP交直线l于点Q,线段BO的中点为E,求证:点B关于直线EF的对称点在直线PF上。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】昆明市某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300),该社团将该校区在2018年100天的空气质量指数监测数据作为样本,绘制的频率分布直方图如图4,把该直方图所得频率估计为概率.
空气质量指数 |
|
|
|
|
|
|
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4度中度污染 | 5度重度污染 | 6级严重污染 |
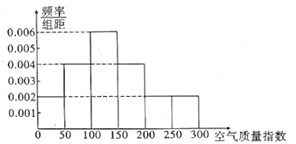
(1)请估算2019年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(2)用分层抽样的方法共抽取10天,则空气质量指数在![]() ,
,![]() ,
,![]() 的天数中各应抽取几天?
的天数中各应抽取几天?
(3)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为2000元,空气质量等级为3级时每天需净化空气的费用为4000元若在(2)的条件下,从空气质量指数在![]() 的天数中任意抽取两天,求这两天的净化空气总费用
的天数中任意抽取两天,求这两天的净化空气总费用![]() 的分布列
的分布列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区不同身高![]() 的未成年男孩的体重平均值
的未成年男孩的体重平均值![]() 如下表:
如下表:
身高 | 60 | 70 | 80 | 90 | 100 |
体重 | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 |
已知![]() 与
与![]() 之间存在很强的线性相关性,
之间存在很强的线性相关性,
(1)据此建立![]() 与
与![]() 之间的回归方程;
之间的回归方程;
(2)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高![]() 体重为
体重为![]() 的在校男生的体重是否正常?
的在校男生的体重是否正常?
参考数据:![]() ,
,![]() ,
,![]()
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 下列结论错误的是
A. 命题:“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”
”
B. “![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C. 命题:“![]() ,
, ![]() ”的否定是“
”的否定是“![]() ,
, ![]() ”
”
D. 若“![]() ”为假命题,则
”为假命题,则![]() 均为假命题
均为假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com