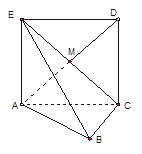
【题目】如图,边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,![]() ,且AC=BC.
,且AC=BC.
(1)求证:![]() 平面EBC;
平面EBC;
(2)求二面角![]() 的大小.
的大小.
参考答案:
【答案】(1)祥见解析;(2)![]() .
.
【解析】试题分析:由已知四边形![]() 是正方形,知其两条对角线互相垂直平分,且
是正方形,知其两条对角线互相垂直平分,且![]() ,又因为平面
,又因为平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故可以以点
,故可以以点![]() 为原点,以过
为原点,以过![]() 点平行于
点平行于![]() 的直线为
的直线为![]() 轴,分别以直线
轴,分别以直线![]() 和
和![]() 为
为![]() 轴和
轴和![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ;又因为正方形ACDE的边长为2,且三角形ABC是以角C为直角的直角三角形,从而就可以写出点A,B,C,E及点M的空间直角坐标;则(1)求出向量
;又因为正方形ACDE的边长为2,且三角形ABC是以角C为直角的直角三角形,从而就可以写出点A,B,C,E及点M的空间直角坐标;则(1)求出向量![]() 的坐标,从而可证
的坐标,从而可证![]() ,这样就可证明直线AM与平面EBC内的两条相交直线垂直,故得直线AM与平面EBC垂直;(2)由(1)知
,这样就可证明直线AM与平面EBC内的两条相交直线垂直,故得直线AM与平面EBC垂直;(2)由(1)知![]() 是平面EBC的一个法向量,其坐标已求,再设平面EAB的一个法向量为
是平面EBC的一个法向量,其坐标已求,再设平面EAB的一个法向量为![]() ,则由
,则由![]() 且
且![]() ,可求得平面EAB的一个法向量;从而可求出所求二面角的两个面的法向量夹角的余弦值,由图可知所求二面角为锐二面角,故二面角的余弦值等于两个面的法向量夹角余弦值的绝对值,从而就可求得所求二面角的大小.另本题也可用几何方法求解证明.
,可求得平面EAB的一个法向量;从而可求出所求二面角的两个面的法向量夹角的余弦值,由图可知所求二面角为锐二面角,故二面角的余弦值等于两个面的法向量夹角余弦值的绝对值,从而就可求得所求二面角的大小.另本题也可用几何方法求解证明.
试题解析:∵四边形![]() 是正方形 ,
是正方形 ,![]() ,
,
∵平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
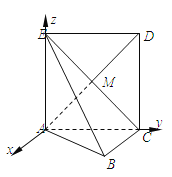
∴可以以点![]() 为原点,以过
为原点,以过![]() 点平行于
点平行于![]() 的直线为
的直线为![]() 轴,
轴,
分别以直线![]() 和
和![]() 为
为![]() 轴和
轴和![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() .
.
设![]() ,则
,则![]()
![]() ,
,
![]() 是正方形
是正方形![]() 的对角线的交点,
的对角线的交点,![]() .
.
(1)![]()
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() 平面
平面![]() .
.
(2) 设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() 且
且![]() ,
,
![]() 且
且![]() .
.
![]() 即
即![]()
取![]() ,则
,则![]() , 则
, 则![]() .
.
又∵![]() 为平面
为平面![]() 的一个法向量,且
的一个法向量,且![]() ,
,
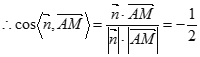 ,
,
设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() ,
,
∴二面角![]() 等于
等于![]() .
.
(1) ,(2)均可用几何法
-
科目: 来源: 题型:
查看答案和解析>>【题目】社会公众人物的言行一定程度上影响着年轻人的人生观、价值观.某媒体机构为了解大学生对影视、歌星以及著名主持人方面的新闻(简称:“星闻”)的关注情况,随机调查了某大学的
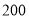 位大学生,得到信息如下表:
位大学生,得到信息如下表: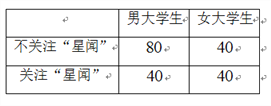
(Ⅰ)从所抽取的
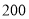 人内关注“星闻”的大学生中,再抽取三人做进一步调查,求这三人性别不全相同的概率;
人内关注“星闻”的大学生中,再抽取三人做进一步调查,求这三人性别不全相同的概率;(Ⅱ)是否有
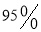 以上的把握认为“关注‘星闻’与性别有关”,并说明理由;
以上的把握认为“关注‘星闻’与性别有关”,并说明理由; (Ⅲ)把以上的频率视为概率,若从该大学随机抽取
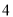 位男大学生,设这
位男大学生,设这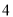 人中关注“星闻”的人数为
人中关注“星闻”的人数为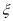 ,求
,求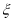 的分布列及数学期望.
的分布列及数学期望.附:
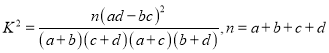 .
.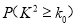
0.050
0.010
0.001
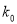
3.841
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车站每天均有3辆开往省城的分为上、中、下等级的客车,某天袁先生准备在该汽车站乘车前往省城办事,但他不知道客车的车况,也不知道发车顺序.为了尽可能乘上上等车,他采取如下策略:先放过一辆,如果第二辆比第一辆好则上第二辆,否则上第三辆.则他乘上上等车的概率为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
周销售量(单位:吨)
2
3
4
频数
20
50
30
⑴ 根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
⑵ 已知每吨该商品的销售利润为2千元,
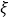 表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求
表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求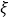 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家用电器公司生产一新款热水器,首先每年需要固定投入 200万元,其次每生产1百台,需再投入0.9万元.假设该公司生产的该款热水器当年能全部售出,但每销售1百台需另付运输费0.1万元.根据以往的经验,年销售总额
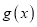 (万元)关于年产量
(万元)关于年产量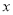 (百台)的函数为
(百台)的函数为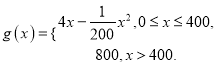 .
.(1)将年利润
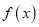 表示为年产量
表示为年产量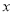 的函数;
的函数;(2)求该公司生产的该款热水器的最大年利润及相应的年产量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)某公司为了解广告投入对销售收益的影响,在若干地区各投入
 万元广告费用,并将各地的销售收益(单位:万元)绘制成如图所示的频率分布直方图.由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益(单位:万元)绘制成如图所示的频率分布直方图.由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从 开始计数的.
开始计数的.

(Ⅰ)根据频率分布直方图计算图中各小长方形的宽度;
(Ⅱ)该公司按照类似的研究方法,测得另外一些数据,并整理得到上表:表中的数据显示
 与
与 之间存在线性相关关系,求
之间存在线性相关关系,求 关于
关于 的回归方程;
的回归方程;(Ⅲ)若广告投入
 万元时,实际销售收益为
万元时,实际销售收益为 .
. 万元,求残差
万元,求残差 .
.
 附:
附: -
科目: 来源: 题型:
查看答案和解析>>【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为
 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:交强险浮动因素和浮动费率比率表
浮动因素
浮动比率
上一个年度未发生有责任道路交通事故
下浮10%
上两个年度未发生有责任道路交通事故
下浮20%

上三个及以上年度未发生有责任道路交通事故
下浮30%
上一个年度发生一次有责任不涉及死亡的道路交通事故
0%
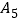
上一个年度发生两次及两次以上有责任道路交通事故
上浮10%
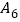
上一个年度发生有责任道路交通死亡事故
上浮30%
某机构为了 某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型
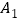
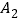

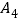
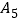
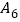
数量
10
5
5
20
15
5
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定,
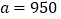 ,记
,记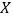 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求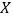 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
相关试题

