设数列{xn}满足lnxn+1=1+lnxn,且x1+x2+x3+…+x10=10.则x21+x22+x23+…+x30的值为( )
A.11•e20
B.11•e21
C.10•e21
D.10•e20
A.11•e20
B.11•e21
C.10•e21
D.10•e20
【答案】分析:由lnxn+1=1+lnxn,可得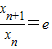 ,由x1+x2+x3+…+x10=10,结合等比数列的通项公式,即可得到结论.
,由x1+x2+x3+…+x10=10,结合等比数列的通项公式,即可得到结论.
解答:解:∵lnxn+1=1+lnxn,
∴lnxn+1-lnxn=1
∴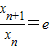
∵x1+x2+x3+…+x10=10
∴x21+x22+x23+…+x30=e20•(x1+x2+x3+…+x10)=10e20,
故选D.
点评:本题考查数列递推式,考查等比数列的通项公式的运用,考查学生的计算能力,属于基础题.
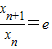 ,由x1+x2+x3+…+x10=10,结合等比数列的通项公式,即可得到结论.
,由x1+x2+x3+…+x10=10,结合等比数列的通项公式,即可得到结论.解答:解:∵lnxn+1=1+lnxn,
∴lnxn+1-lnxn=1
∴
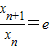
∵x1+x2+x3+…+x10=10
∴x21+x22+x23+…+x30=e20•(x1+x2+x3+…+x10)=10e20,
故选D.
点评:本题考查数列递推式,考查等比数列的通项公式的运用,考查学生的计算能力,属于基础题.

