【题目】已知函数![]() .
.
(1)当![]() ,且
,且![]() 是
是![]() 上的增函数,求实数
上的增函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() ,且对任意实数
,且对任意实数![]() ,关于
,关于![]() 的方程
的方程![]() 总有三个不相等的实数根,求实数
总有三个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)分类讨论将![]() 中的绝对值号去掉,再根据二次函数的性质得到关于
中的绝对值号去掉,再根据二次函数的性质得到关于![]() 的不等式组,即可求解;(2)
的不等式组,即可求解;(2)![]() 是由两个二次函数构成的分段函数,对
是由两个二次函数构成的分段函数,对![]() 的取值讨论两个二次函数对称轴的位置,结合二次函数的性质,再利用函数图象,即可求解.
的取值讨论两个二次函数对称轴的位置,结合二次函数的性质,再利用函数图象,即可求解.
试题解析:(1)![]() ,由于
,由于![]() 在
在![]() 上递增,
上递增,
∴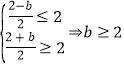 ;(2)
;(2)![]() ,∵
,∵![]() ,两对称轴分别是
,两对称轴分别是![]() ,
,
①当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增,
上递增,![]() ,
,![]() ,由题得
,由题得 ,对
,对![]() 恒成立,即
恒成立,即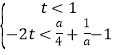 ,对
,对![]() 恒成立,而
恒成立,而![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增,
上递增,![]() ,
,![]() ,由题得
,由题得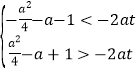 ,对
,对![]() 恒成立,即
恒成立,即![]() ,对
,对![]() 恒成立,
恒成立,
对![]() 对
对![]() 恒成立得,
恒成立得,![]() 或
或![]() ,或
,或![]() ,
,
∴![]() ,同理对
,同理对![]() ,对
,对![]() 恒成立,得
恒成立,得![]() ,∴当
,∴当![]() 时,
时,![]() ;
;
综上,由①②可知,所求的范围是![]() .
.

