【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)当![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(2)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,若
,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“类对称点”,当
的“类对称点”,当![]() 时,试问
时,试问![]() 是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)先求得定义域![]() 求导得
求导得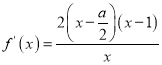 ,由于
,由于![]() ,所以增区间为
,所以增区间为![]() ;(2)当
;(2)当![]() 时,
时,![]() ,利用导数求得切线
,利用导数求得切线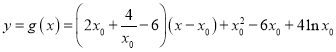 ,两式相减得
,两式相减得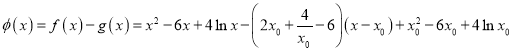 ,利用导数求得以当
,利用导数求得以当![]() 时,
时,![]() 存在“类对称点”.
存在“类对称点”.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]() ,∵
,∵![]() ,∴
,∴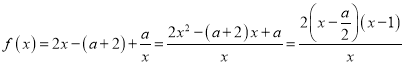 ,∵
,∵![]() ,∴
,∴![]() ,令
,令![]() ,即
,即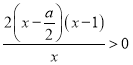 ,∵
,∵![]() ,∴
,∴![]() 或
或![]() ,
,
所以函数![]() 的单调递增区间是
的单调递增区间是![]() ;
;
(2)当![]() 时,
时,![]() ,
,
∴![]() ,
,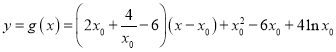 ,
,
令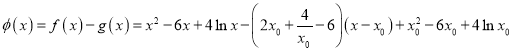 ,
,
则![]() ,
,
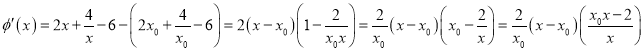 ,当
,当![]() 时,
时,![]() 在
在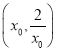 上单调递减.
上单调递减.
∴当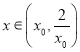 时,
时,![]() ,
,
从而有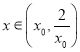 时,
时,![]() ,
,
当![]() 时,
时,![]() 在
在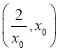 上单调递减,
上单调递减,
∴当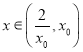 时,
时,![]() ,
,
从而有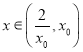 时,
时,![]() ,
,
∴当![]() 时,
时,![]() 不存在“类对称点”.
不存在“类对称点”.
当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上是增函数,故
上是增函数,故![]() ,
,
所以当![]() 时,
时,![]() 存在“类对称点”.
存在“类对称点”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大学餐饮中心为了了解新生的饮食习惯,利用简单随机抽样的方法在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品
不喜欢甜品
合计
南方学生
60
20
80
北方学生
10
10
20
合计
70
30
100
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)根据(1)的结论,你能否提出更好的调查方法来了解该校大学新生的饮食习惯,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】衡州市临枣中学高二某小组随机调查芙蓉社区160个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,得到下面的数据表:
休闲方式
性别
看电视
看书
合计
男
20
100
120
女
20
20
40
合计
40
120
160
下面临界值表:
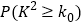
0.15
0.10
0.05
0.025
0.010
0.005
0.001
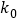
2.072
2.706
3.841
5.024
6.635
7.879
10.828
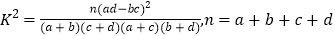
(Ⅰ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量
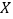 ,求
,求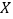 的分别列和期望;
的分别列和期望;(Ⅱ)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
-
科目: 来源: 题型:
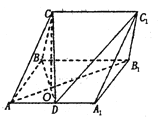
查看答案和解析>>【题目】在三棱柱中
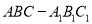 中,侧面
中,侧面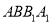 为矩形,
为矩形, 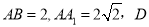 是
是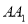 的中点,
的中点, 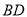 与
与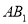 交于点
交于点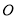 ,且
,且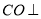 平面
平面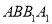 .
.
(1)证明:
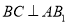 ;
;(2)若
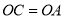 ,求直线
,求直线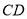 与平面
与平面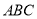 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如下,已知分数在100~110的学生数有21人。

(Ⅰ)求总人数N和分数在110~115分的人数n;
(Ⅱ)现准备从分数在110~115分的n名学生(女生占
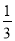 )中任选2人,求其中恰好含有一名女生的概率;
)中任选2人,求其中恰好含有一名女生的概率;(Ⅲ)为了分析某个学生的学习状态,对其下一阶段的学习提供指导性建议,对他前7次考试的数学成绩x(满分150分),物理成绩y进行分析,下面是该生7次考试的成绩。
数学
88
83
117
92
108
100
112
物理
94
91
108
96
104
101
106
已知该生的物理成绩y与数学成绩x是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据
 其回归线
其回归线 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年12月16日,科幻片《侠盗一号》上映,上映至今,全球累计票房高达8亿美金.为了了解娄底观众的满意度,某影院随机调查了本市观看影片的观众,并用“10分制”对满意度进行评分,分数越高满意度越高,若分数不低于9分,则称该观众为“满意观众”.现从调查人群中随机抽取12名.如图所示的茎叶图记录了他们的满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).
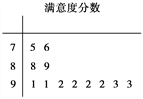
(1)求从这12人中随机选取1人,该人不是“满意观众”的概率;
(2)从本次所记录的满意度评分大于9.1的“满意观众”中随机抽取2人,求这2人得分不同的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了参加师大附中第30届田径运动会的开幕式,高三年级某6个班联合到集市购买了6根竹竿,作为班期的旗杆之用,它们的长度分别为3.8,4.3,3.6,4.5,4.0,4.1(单位:米).
(1)若从中随机抽取两根竹竿,求长度之差不超过0.5米的概率;
(2)若长度不小于4米的竹竿价格为每根10元,长度小于4米的竹竿价格为每根
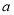 元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求
元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求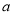 的值.
的值.
相关试题

