直线y=a与函数y=x3-3x的图象有相异三个交点,则a的取值范围是
- A.(-2,2)
- B.(-2,0)
- C.(0,2)
- D.(2,+∞)
A
分析:先求出函数与x轴的交点,然后利用导数求出函数的极值,结合函数y=x3-3x的图象与y=a的图象,观察即可求出满足条件的a.
解答:y=x3-3x=x(x2-3)=0
解得方程有三个根分别为 ,0,
,0,
y'=3x2-3=0解得,x=1或-1
f(1)=-2,f(-1)=2
画出函数y=x3-3x的图象与y=a
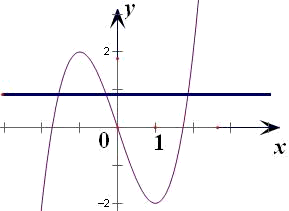
观察图象可得a∈(-2,2)
故选A.
点评:本题主要考查了利用导数研究函数的极值,以及数形结合的思想,属于基础题.
分析:先求出函数与x轴的交点,然后利用导数求出函数的极值,结合函数y=x3-3x的图象与y=a的图象,观察即可求出满足条件的a.
解答:y=x3-3x=x(x2-3)=0
解得方程有三个根分别为
 ,0,
,0,
y'=3x2-3=0解得,x=1或-1
f(1)=-2,f(-1)=2
画出函数y=x3-3x的图象与y=a

观察图象可得a∈(-2,2)
故选A.
点评:本题主要考查了利用导数研究函数的极值,以及数形结合的思想,属于基础题.

