函数f(x)=-x2+2ax与g(x)=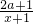 在区间[1,2]上都是减函数,则a的取值范围是
在区间[1,2]上都是减函数,则a的取值范围是
- A.(-
 ,1]
,1] - B.(
 ,0)∪(0,1)
,0)∪(0,1) - C.(-
 ,0)∪(0,1]
,0)∪(0,1] - D.(-
 ,1)
,1)
A
分析:根据二次函数的单调性,得[1,2]必定是[a,+∞)的子集,从而得到a≤1.由分式函数的单调性,得g(x)=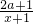 在2a+1>0时在区间[1,2]上是减函数,可得a
在2a+1>0时在区间[1,2]上是减函数,可得a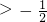 ,最后综合,可得实数a的取值范围.
,最后综合,可得实数a的取值范围.
解答:∵函数f(x)=-x2+2ax的单调减区间是[a,+∞)
∴若f(x)=-x2+2ax区间[1,2]上是减函数,则a≤1
又∵g(x)=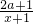 当2a+1>0时在区间(-1,+∞)上是减函数,而[1,2]⊊(-1,+∞)
当2a+1>0时在区间(-1,+∞)上是减函数,而[1,2]⊊(-1,+∞)
∴若g(x)=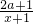 在区间[1,2]上是减函数,则2a+1>0,得a
在区间[1,2]上是减函数,则2a+1>0,得a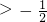
综上所述,得a的取值范围是(- ,1]
,1]
故选:A
点评:本题给出含有参数的分式函数与二次函数有共同的单调减区间,求参数a的取值范围,着重考查了基本初等函数的单调性与单调区间求法等知识,属于基础题.
分析:根据二次函数的单调性,得[1,2]必定是[a,+∞)的子集,从而得到a≤1.由分式函数的单调性,得g(x)=
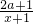 在2a+1>0时在区间[1,2]上是减函数,可得a
在2a+1>0时在区间[1,2]上是减函数,可得a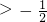 ,最后综合,可得实数a的取值范围.
,最后综合,可得实数a的取值范围.解答:∵函数f(x)=-x2+2ax的单调减区间是[a,+∞)
∴若f(x)=-x2+2ax区间[1,2]上是减函数,则a≤1
又∵g(x)=
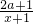 当2a+1>0时在区间(-1,+∞)上是减函数,而[1,2]⊊(-1,+∞)
当2a+1>0时在区间(-1,+∞)上是减函数,而[1,2]⊊(-1,+∞)∴若g(x)=
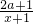 在区间[1,2]上是减函数,则2a+1>0,得a
在区间[1,2]上是减函数,则2a+1>0,得a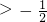
综上所述,得a的取值范围是(-
 ,1]
,1]故选:A
点评:本题给出含有参数的分式函数与二次函数有共同的单调减区间,求参数a的取值范围,着重考查了基本初等函数的单调性与单调区间求法等知识,属于基础题.

