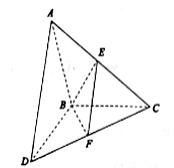
【题目】如图所示,![]() 和
和![]() 所在平面互相垂直,且
所在平面互相垂直,且![]() 分别为
分别为![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)以![]() 为坐标原点,在平面
为坐标原点,在平面![]() 内过
内过![]() 作垂直
作垂直![]() 的直线,并将其作为
的直线,并将其作为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,在平面
轴,在平面![]() 内过
内过![]() 作垂直
作垂直![]() 的直线,并将其作为
的直线,并将其作为![]() 轴,建立如图所示空间直角坐标系,利用向量的运算,即可证得
轴,建立如图所示空间直角坐标系,利用向量的运算,即可证得![]() ;(2)求得平面
;(2)求得平面![]() 的一个法向量为
的一个法向量为![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,利用法向量所成的角,即可求解二面角的大小.
,利用法向量所成的角,即可求解二面角的大小.
试题解析:(1)证明:由题意,以![]() 为坐标原点,在平面
为坐标原点,在平面![]() 内过
内过![]() 作垂直
作垂直![]() 的直线,并将其作为
的直线,并将其作为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,在平面
轴,在平面![]() 内过
内过![]() 作垂直
作垂直![]() 的直线,并将其作为
的直线,并将其作为![]() 轴,建立如图所示空间直角坐标系,易得
轴,建立如图所示空间直角坐标系,易得![]() ,因而
,因而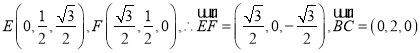 ,
,
因此![]() ,从而
,从而![]() .
.
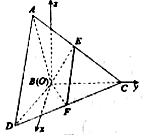
(2)在图中,平面![]() 的一个法向量为
的一个法向量为![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,
,
又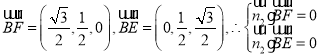 ,得其中一个
,得其中一个![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,且由题知
,且由题知![]() 为锐角,
为锐角,
则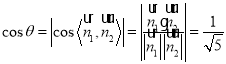 ,因此
,因此![]() ,
,
即所求二面角正弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四棱锥
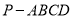 中,底面
中,底面 是正方形,
是正方形, 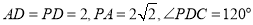 .
.(1)如图2,设点
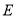 为
为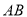 的中点,点
的中点,点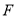 为
为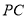 的中点,求证:
的中点,求证:  平面
平面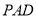 ;
;(2)已知网格纸上小正方形的边长为
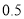 ,请你在网格纸上用粗线画图1中四棱锥
,请你在网格纸上用粗线画图1中四棱锥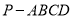 的府视图(不需要标字母),并说明理由.
的府视图(不需要标字母),并说明理由.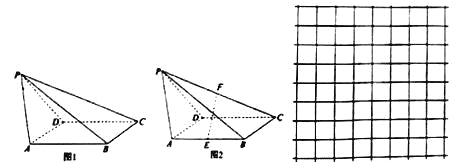
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,点
,点 为坐标原点,若椭圆
为坐标原点,若椭圆 与曲线
与曲线 的交点分别为
的交点分别为 (
( 下
下 上),且
上),且 两点满足
两点满足 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过椭圆
 上异于其顶点的任一点
上异于其顶点的任一点 ,作
,作 的两条切线,切点分别为
的两条切线,切点分别为 ,且直线
,且直线 在
在 轴、
轴、 轴上的截距分别为
轴上的截距分别为 ,证明:
,证明: 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正三棱柱
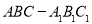 (侧棱垂直于底面,且底面是正三角形)中,
(侧棱垂直于底面,且底面是正三角形)中,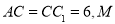 是棱
是棱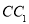 上一点.
上一点.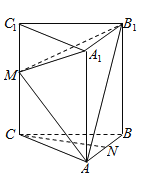
(1)若
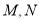 分别是
分别是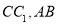 的中点,求证:
的中点,求证: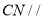 平面
平面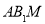 ;
; (2)若
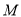 是
是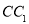 上靠近点
上靠近点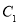 的一个三等分点,求二面角
的一个三等分点,求二面角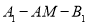 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,点
,点 为坐标原点,若椭圆
为坐标原点,若椭圆 与曲线
与曲线 的交点分别为
的交点分别为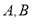 (
( 下
下 上),且
上),且 两点满足
两点满足 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过椭圆
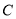 上异于其顶点的任一点
上异于其顶点的任一点 ,作
,作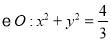 的两条切线,切点分别为
的两条切线,切点分别为 ,且直线
,且直线 在
在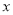 轴、
轴、 轴上的截距分别为
轴上的截距分别为 ,证明:
,证明: 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】时下,租车已经成为新一代的流行词,租车自驾游也慢慢流行起来,某小车租车点的收费标准是,不超过2天按照300元计算;超过两天的部分每天收费标准为100元(不足1天的部分按1天计算).有甲乙两人相互独立来该租车点租车自驾游(各租一车一次),设甲、乙不超过2天还车的概率分别为
 ;2天以上且不超过3天还车的概率分别
;2天以上且不超过3天还车的概率分别 ;两人租车时间都不会超过4天.
;两人租车时间都不会超过4天.(1)求甲所付租车费用大于乙所付租车费用的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量
 ,求
,求 的分布列与数学期望
的分布列与数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,其中
,其中 .
.(1)若
 是函数
是函数 的极值点,求
的极值点,求 的值;
的值;(2)求
 的单调区间;
的单调区间;(3)若
 在
在 上的最大值是0,求
上的最大值是0,求 的取值范围.
的取值范围.
相关试题

