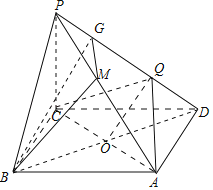
【题目】已知四棱锥P﹣ABCD中，底面ABCD为平行四边形，点M，N，Q分别在PA，BD，PD上.

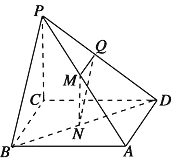
（1）若PM：MA＝BN：ND＝PQ：QD，求证：平面MNQ∥平面PBC.

（2）若Q满足PQ：QD＝2，则M点满足什么条件时，BM∥面AQC.

【答案】（1）证明见解析（2）M为PA的中点

【解析】

利用线面平行的判定定理证明MQ∥平面PBC, QN∥平面PBC,然后面面平行的判定定理即可证明;

连接AC，交BD于O，连接OQ，取PQ的中点G，连接BG，利用线面平行的判定定理可证BG∥平面AQC,取PA的中点M，连接GM,同理可证, GM∥平面AQC,再由面面平行的判定定理证明平面BGM∥平面AQC,再由面面平行的性质即可得证.

（1）证明：∵PM：MA＝PQ：QD.

∴QM∥AD，∵AD∥BC，∴QM∥BC，

∵ 平面PBC，BC平面PBC，

∴MQ∥平面PBC,

∵BN：ND＝PQ：QD.∴QN∥PB，

平面,平面,

QN∥平面PBC,

∵QM∩QN＝Q，∴平面MNQ∥平面PBC；

（2）当M点为PA的中点时，BM∥面AQC

证明如下:连接AC，交BD于O，连接OQ，

取PQ的中点G，连接BG，则BG∥OQ，

∵OQ平面AQC，BG平面AQC，∴BG∥平面AQC，

取PA的中点M，连接GM，则GM∥AQ，

∵AQ平面AQC，GM平面AQC，∴GM∥平面AQC，

又BG∩GM＝G，∴平面BGM∥平面AQC，

则BM∥面AQC，此时M为PA的中点.

关闭