
【题目】在正方体![]() 中,
中,![]() 、
、![]() 分别在
分别在![]() 和
和![]() 上(异于端点),则过三点
上(异于端点),则过三点![]() 、
、![]() 、
、![]() 的平面被正方体截得的图形不可能是( )
的平面被正方体截得的图形不可能是( )
A.正方形B.不是正方形的菱形
C.不是正方形的矩形D.梯形
【答案】A
【解析】
作出图形,设正方体的棱长为![]() ,设
,设![]() ,利用勾股定理可判断A选项中的截面图形不可能,结合A选项的推导可判断B选项中的截面图形可能,取
,利用勾股定理可判断A选项中的截面图形不可能,结合A选项的推导可判断B选项中的截面图形可能,取![]() 可判断C选项中图形可能,取
可判断C选项中图形可能,取![]() 可判断D选项中截面图形可能.综合可得出结论.
可判断D选项中截面图形可能.综合可得出结论.
对于A选项,设正方体![]() 的棱长为
的棱长为![]() ,如下图所示:
,如下图所示:
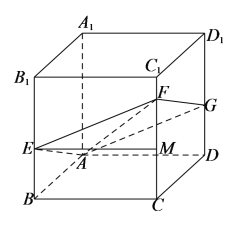
设![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,同理
,同理![]() ,
,
若截面![]() 为正方形,则
为正方形,则![]() ,
,
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,易知
,易知![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
由勾股定理得![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以,截面不可能是正方形;
对于B选项,由A选项可知,当![]() 时,截面是不为正方形的菱形;
时,截面是不为正方形的菱形;
对于C选项,如下图所示,当![]() 时,由于
时,由于![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,由面面平行的性质定理可得
,由面面平行的性质定理可得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
此时,四边形![]() 为矩形但不是正方形;
为矩形但不是正方形;
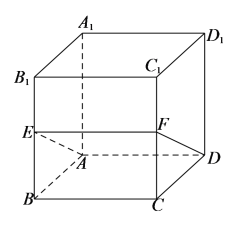
对于D选项,如下图所示,
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,由面面平行的性质定理可得
,由面面平行的性质定理可得![]() ,
,
当![]() 时,过点
时,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,易知
,易知![]() 且
且![]() ,
,
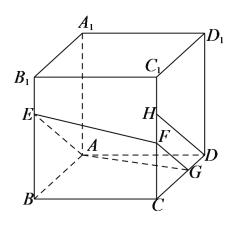
此时,截面图形为梯形.
故选:A.


科目:高中数学 来源: 题型:
【题目】如图,在直角![]() 中,
中,![]() ,
,![]() 通过
通过![]() 以直线
以直线![]() 为轴顺时针旋转
为轴顺时针旋转![]() 得到(
得到(![]() ).点
).点![]() 为斜边
为斜边![]() 上一点.点
上一点.点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)当直线![]() 与平面
与平面![]() 所成的角取最大值时,求二面角
所成的角取最大值时,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:y2=2px(p>0)的焦点为F,准线为l,AB为过焦点F且垂直于x轴的抛物线C的弦,已知以AB为直径的圆经过点(-1,0).
(1)求p的值及该圆的方程;
(2)设M为l上任意一点,过点M作C的切线,切点为N,证明:MF⊥NF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,
, 为椭圆C上一点.
为椭圆C上一点.
(1)求椭圆C的方程;
(2)设椭圆C的左、右顶点分别为![]() ,
,![]() ,过
,过![]() ,
,![]() 分别作x轴的垂线
分别作x轴的垂线![]() ,
,![]() ,椭圆C的一条切线
,椭圆C的一条切线![]() 与
与![]() ,
,![]() 交于M,N两点,求证:
交于M,N两点,求证:![]() 是定值.
是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.若曲线
轴的正半轴为极轴建立极坐标系.若曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 点的极坐标为
点的极坐标为![]() ,在平面直角坐标系中直线
,在平面直角坐标系中直线![]() 经过点
经过点![]() ,且倾斜角为
,且倾斜角为![]() .
.
(1)写出曲线![]() 的直角坐标方程以及点
的直角坐标方程以及点![]() 的直角坐标;
的直角坐标;
(2)设直线与曲线![]() 相交于
相交于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
:![]() 与抛物线
与抛物线![]() 切于点
切于点![]() ,直线
,直线![]() :
:![]() 过定点Q,且抛物线
过定点Q,且抛物线![]() 上的点到点Q的距离与其到准线距离之和的最小值为
上的点到点Q的距离与其到准线距离之和的最小值为![]() .
.
(1)求抛物线![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(2)设直线![]() 与抛物线
与抛物线![]() 交于(异于点P)两个不同的点A、B,直线PA,PB的斜率分别为
交于(异于点P)两个不同的点A、B,直线PA,PB的斜率分别为![]() ,那么是否存在实数
,那么是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】百年大计,教育为本.某校积极响应教育部号召,不断加大拔尖人才的培养力度,为清华、北大等排名前十的名校输送更多的人才.该校成立特长班进行专项培训.据统计有如下表格.(其中![]() 表示通过自主招生获得降分资格的学生人数,
表示通过自主招生获得降分资格的学生人数,![]() 表示被清华、北大等名校录取的学生人数)
表示被清华、北大等名校录取的学生人数)
年份(届) | 2014 | 2015 | 2016 | 2017 | 2018 |
| 41 | 49 | 55 | 57 | 63 |
| 82 | 96 | 108 | 106 | 123 |
(1)通过画散点图发现![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(保留两位有效数字)
的线性回归方程;(保留两位有效数字)
(2)若已知该校2019年通过自主招生获得降分资格的学生人数为61人,预测2019年高考该校考人名校的人数;
(3)若从2014年和2018年考人名校的学生中采用分层抽样的方式抽取出5个人回校宣传,在选取的5个人中再选取2人进行演讲,求进行演讲的两人是2018年毕业的人数![]() 的分布列和期望.
的分布列和期望.
参考公式: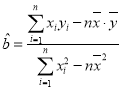 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com