【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且a＋b＋c＝8.

(1)若a＝2，b＝，求cosC的值；

(2)若sinAcos2＋sinB·cos2＝2sinC，且△ABC的面积S＝sinC，求a和b的值．

【答案】(1) (2) a＝3，b＝3.

【解析】

试题分析: （1）利用三角形的周长求出 ，利用余弦定理求解即可．
（2）由已知可得 利用正弦定理，结合已知条件三角形的面积，求解即可．

试题解析：( (1)由题意可知c＝8－(a＋b)＝.

由余弦定理得cosC＝＝＝－.

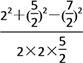(2)由sinAcos2＋sinBcos2＝2sinC，可得

sinA·＋sinB·＝2sinC，

化简得sinA＋sinAcosB＋sinB＋sinBcosA＝4sinC.

因为sinAcosB＋cosAsinB＝sin(A＋B)＝sinC，所以sinA＋sinB＝3sinC.

由正弦定理可知a＋b＝3c.又因为a＋b＋c＝8，故a＋b＝6.

由于S＝absinC＝sinC，所以ab＝9，从而a2－6a＋9＝0，解得a＝3，b＝3.

关闭