【题目】提高过江大桥的车辆通行的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度![]() (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度![]() (单位:辆/千米)
(单位:辆/千米)
的函数.当桥上的车流密度达到200辆/千米时,就会造成堵塞,此时车流速度为0;当
车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当![]() 时,
时,
车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)如果车流量(单位时间内通过桥上某观测点的车辆数)![]() (单位:辆/小时),那么当车流密度
(单位:辆/小时),那么当车流密度![]() 为多大时,车流量
为多大时,车流量![]() 可以达到最大,并求出最大值.(精确到
可以达到最大,并求出最大值.(精确到![]() 辆/小时).
辆/小时).
参考答案:
【答案】(1)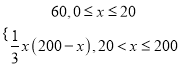 ;(2)
;(2)![]()
![]() .
.
【解析】试题分析:
本题考查函数模型在实际中的应用以及分段函数最值的求法。(1)根据题意用分段函数并结合待定系数法求出函数的关系式。(2)首先由题意得到![]() 的解析式,再根据分段函数最值的求得求得最值即可。
的解析式,再根据分段函数最值的求得求得最值即可。
试题解析:
(1)由题意:当![]() 时,
时, ![]() ;
;
当![]() 时,设
时,设![]()
由已知得![]() 解得
解得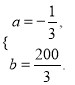
∴![]() 。
。
综上可得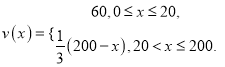
(2)依题意并由(1)可得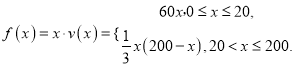
①当![]() 时,
时, ![]() 为增函数,
为增函数,
∴当![]() 时,
时, ![]() 取得最大值,且最大值为
取得最大值,且最大值为![]() 1200 。
1200 。
②当![]() 时,
时, ![]() ,
,
∴当![]() 时,
时, ![]() 取得最大值,且最大值为
取得最大值,且最大值为![]() 。
。
所以![]() 的最大值为
的最大值为![]() 。
。
故当车流密度为100辆/千米时,车流量可以达到最大,且大值为3333辆/小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a≥0,试讨论函数g(x)=lnx+ax2﹣(2a+1)x在(0,+∞)上的单调性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合
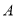 =
=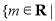 幂函数
幂函数 =
=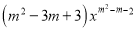 的图象不过原点
的图象不过原点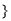 ,则集合A的真子集的个数为
,则集合A的真子集的个数为A. 1 B. 2 C. 3 D. 无数
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了预防甲型
 流感,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时室内每立方米空气中的含药量
流感,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时室内每立方米空气中的含药量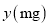 与时间
与时间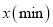 成正比例,药物燃烧完后满足
成正比例,药物燃烧完后满足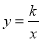 ,如图所示,现测得药物8
,如图所示,现测得药物8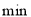 燃毕,此时室内空气中每立方米的含药量为6
燃毕,此时室内空气中每立方米的含药量为6 ,请按题中所供给的信息,解答下列各题.
,请按题中所供给的信息,解答下列各题.
(1)求
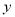 关于
关于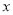 的函数解析式;
的函数解析式;(2)研究表明,当空气中每立方米的含药量不低于
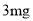 且持续时间不低于
且持续时间不低于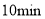 时才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
时才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】设z1 , z2是复数,给出下列四个命题: ①若|z1﹣z2|=0,则
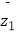 =
= 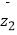 ②若z1=
②若z1= 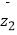 ,则
,则 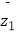 =z2
=z2
③若|z1|=|z2|,则z1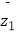 =z2
=z2 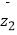 ④若|z1|=|z2|,则z12=z22
④若|z1|=|z2|,则z12=z22
其中真命题的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
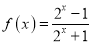 .
.(1)判断函数
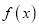 的奇偶性;
的奇偶性;(2)判断并证明
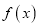 )在
)在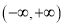 )上的单调性;
)上的单调性;(3)若
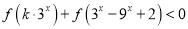 对任意
对任意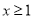 恒成立,求
恒成立,求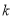 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx,g(x)=f(x)+ax2+bx,其中函数g(x)的图象在点(1,g(1))处的切线平行于x轴.
(1)确定a与b的关系;
(2)若a≥0,试讨论函数g(x)的单调性.
相关试题

