【题目】在平面直角坐标系中，以为极点，轴的非负半轴为极轴，建立极坐标系，曲线的极坐标方程为，直线的参数方程为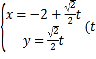为参数，直线与曲线分别交于两点.

（1）若点的极坐标为，求的值；

（2）求曲线的内接矩形周长的最大值.

【答案】（1）4；（2）16.

【解析】

（1）根据题意，将曲线C的极坐标方程变形为标准方程，将直线的参数方程与曲线C的方程联立，可得，由一元二次方程根与系数的关系计算可得答案；

（2）写出曲线C的参数方程，分析可得以P为顶点的内接矩形周长l，由正弦函数的性质分析可得答案．

（1）由，将x=ρcosθ，y=ρsinθ代入得到+3=12,

所以曲线C的直角坐标方程为+3=12，的极坐标为，化为直角坐标为（-2，0）

由直线l的参数方程为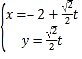：（t为参数），

知直线l是过点P（-2，0），且倾斜角为的直线，

把直线的参数方程代入曲线C得，．

所以|PM||PN|＝|t1t2|＝4．

（2）由曲线C的方程为 ，

不妨设曲线C上的动点，

则以P为顶点的内接矩形周长l，

又由sin（θ）≤1，则l≤16；

因此该内接矩形周长的最大值为16．

关闭