【题目】已知函数y=f(x)是定义在R上的奇函数,且当x≥0时,f(x)=-x2+ax.
(1)若a=-2,求函数f(x)的解析式;
(2)若函数f(x)为R上的单调减函数,
①求a的取值范围;
②若对任意实数m,f(m-1)+f(m2+t)<0恒成立,求实数t的取值范围.
参考答案:
【答案】(1) ![]() .
.
(2) ①a≤0. ②t> ![]() .
.
【解析】
本试题主要是考查了抽象函数的解析式的求解和单调性的证明以及解不等式。
(1)因为当![]() 时,
时,![]() ,又因为
,又因为![]() 为奇函数,所以
为奇函数,所以![]() ,进而得到解析式。
,进而得到解析式。
(2)根据函数单调性,对于参数a分为正负来讨论得到取值范围。
(3)因为![]() ,∴
,∴![]()
所以![]() 是奇函数,∴
是奇函数,∴![]() ,而又因为
,而又因为![]() 为
为![]() 上的单调递减函数,所以
上的单调递减函数,所以![]() 恒成立,分离参数的思想得到范围。
恒成立,分离参数的思想得到范围。
(1)当![]() 时,
时,![]() ,又因为
,又因为![]() 为奇函数,
为奇函数,
所以![]()
所以![]() …………………………6分
…………………………6分
(2)①当![]() 时,对称轴
时,对称轴![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
由于奇函数关于原点对称的区间上单调性相同,所以![]() 在
在![]() 上单调递减,
上单调递减,
又在![]() 上
上![]() ,在
,在![]() 上
上![]() ,
,
所以当a![]() 0时,
0时,![]() 为R上的单调递减函数
为R上的单调递减函数
当a>0时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,不合题意
上递减,不合题意
所以函数![]() 为单调函数时,a的范围为a
为单调函数时,a的范围为a![]() ………………………………………….10分
………………………………………….10分
②因为![]() ,∴
,∴![]()
所以![]() 是奇函数,∴
是奇函数,∴![]() …………………………12分
…………………………12分
又因为![]() 为
为![]() 上的单调递减函数,所以
上的单调递减函数,所以![]() 恒成立,…………………14分
恒成立,…………………14分
所以![]() 恒成立, 所以
恒成立, 所以![]() …………………………16分
…………………………16分
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学从高三男生中随机抽取
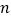 名学生的身高,将数据整理,得到的频率分布表如下所示,
名学生的身高,将数据整理,得到的频率分布表如下所示,组号
分组
频数
频率
第1组
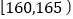
5
0.050
第2组
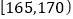
0.350
第3组

30
第4组
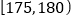
20
0.200
第5组
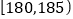
10
0.100
合计
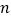
1.00
(Ⅰ)求出频率分布表中①和②位置上相应的数据,并完成下列频率分布直方图;
(Ⅱ)为了能对学生的体能做进一步了解,该校决定在第3,4,5组中用分层抽样抽取6名学生进行不同项目的体能测试,若在这6名学生中随机抽取2名学生进行引体向上测试,则第4组中至少有一名学生被抽中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式|2x﹣1|﹣|x+a|≥a对任意的实数x恒成立,则实数a的取值范围是( )
A.(﹣∞,﹣ ]
]
B.(﹣ ,﹣
,﹣  ]
]
C.(﹣ ,0)
,0)
D.(﹣∞,﹣ ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的最大值为
的最大值为 .
.(Ⅰ)求常数
 的值;
的值;(Ⅱ)求函数
 的单调递增区间;
的单调递增区间;(Ⅲ)若将
 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+bx+1(a,b为实数),设
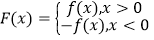 ,
,(1)若f(-1)=0,且对任意实数x均有f(x)≥0成立,求F(x)的表达式;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(3)设mn<0,m+n>0,a>0,且f(x)满足f(-x)=f(x),试比较F(m)+F(n)的值与0的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某创业投资公司拟开发某种新能源产品,估计能获得
 万元到
万元到 万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金
万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金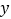 (单位:万元)随投资收益
(单位:万元)随投资收益 (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过 万元,同时奖金不超过收益的
万元,同时奖金不超过收益的 .
.(
 )请分析函数
)请分析函数 是否符合公司要求的奖励函数模型,并说明原因.
是否符合公司要求的奖励函数模型,并说明原因.(
 )若该公司采用函数模型
)若该公司采用函数模型 作为奖励函数模型,试确定最小正整数
作为奖励函数模型,试确定最小正整数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
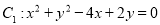 与圆
与圆 .
.(1)求证两圆相交;
(2)求两圆公共弦所在直线的方程;
(3)求过两圆的交点且圆心在直线
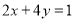 上的圆的方程.
上的圆的方程.
相关试题

