【题目】下列说法正确的是( )
A.回归直线
至少经过其样本数据
中的一个点
B.从独立性检验可知有99%的把握认为吃地沟油与患胃肠癌有关系时，我们就说如果某人吃地沟油，那么他有99%可能患胃肠癌
C.在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高
D.将一组数据的每一个数据都加上或减去同一个常数后，其方差也要加上或减去这个常数
孟建平小学滚动测试系列答案科目：高中数学 来源： 题型：
【题目】为了调查全市学生的数学高考成绩，随机地抽取某中学甲、乙两班各10名同学，获得成绩数据如下（单位：分）.
甲：132，108，112，121，113，121，118，128，118，129；
乙：133，107，120，113，122，114，128，118，129，127.
(1)画出甲、乙两班学生数学成绩的茎叶图，并根据茎叶图判断哪个班的平均水平较高；
(2)若数学成绩不低于120分，则称为“优秀”，求从这20名学生中随机选取三人，至多有一人是优秀的概率；
(3)以这20人的样本数据来估计整个学校的总体成绩，若从该校（人数很多）任选三人，记
表示抽到优秀学生的人数，求的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】先后2次抛掷一枚骰子，将得到的点数分别记为
，
.
（1）求直线
与圆
相切的概率；
（2）将，，5的值分别作为三条线段的长，求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，直线
的参数方程为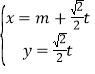
（
为参数），以坐标原点
为极点，
轴正半轴为极轴建立极坐标系，椭圆
的极坐标方程为
，其左焦点
在直线上.
（1）若直线与椭圆交于
两点，求
的值；
（2）求椭圆的内接矩形面积的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个盒子里装有大小均匀的
个小球，其中有红色球
个，编号分别为
；白色球
个, 编号分别为
, 从盒子中任取
个小球（假设取到任何—个小球的可能性相同）．
（1）求取出的个小球中，含有编号为的小球的概率；
（2）在取出的个小球中, 小球编号的最大值设为
，求随机变量的分布列．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点
是圆
：
上一动点，线段
与圆
：
相交于点
.直线
经过，并且垂直于
轴，在上的射影点为
.
（1）求点的轨迹
的方程；
（2）设圆与轴的左、右交点分别为
，
，点
是曲线上的点（点与，不重合），直线
，
与直线
：
分别相交于点
，
，求证：以
直径的圆经过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
