(本小题满分14分)已知函数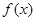 定义在区间
定义在区间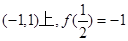 ,对任意
,对任意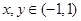 ,恒有
,恒有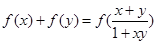 成立,又数列
成立,又数列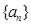 满足
满足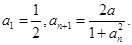 (I)在(-1,1)内求一个实数t,使得
(I)在(-1,1)内求一个实数t,使得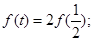 (II)求证:数列
(II)求证:数列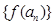 是等比数列,并求
是等比数列,并求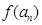 的表达式;(III)设
的表达式;(III)设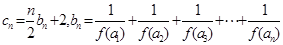 ,是否存在
,是否存在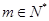 ,使得对任意
,使得对任意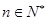 ,
,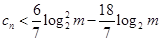 恒成立?若存在,求出m的最小值;若不存在,请说明理由。
恒成立?若存在,求出m的最小值;若不存在,请说明理由。
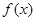 定义在区间
定义在区间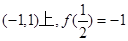 ,对任意
,对任意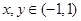 ,恒有
,恒有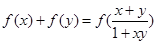 成立,又数列
成立,又数列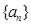 满足
满足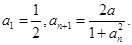 (I)在(-1,1)内求一个实数t,使得
(I)在(-1,1)内求一个实数t,使得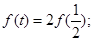 (II)求证:数列
(II)求证:数列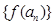 是等比数列,并求
是等比数列,并求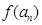 的表达式;(III)设
的表达式;(III)设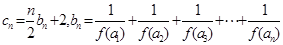 ,是否存在
,是否存在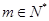 ,使得对任意
,使得对任意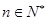 ,
,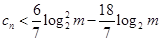 恒成立?若存在,求出m的最小值;若不存在,请说明理由。
恒成立?若存在,求出m的最小值;若不存在,请说明理由。(I) ,∴
,∴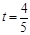 ……2分
……2分
(II)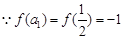 ,且
,且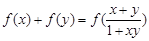
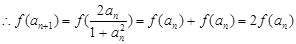 ,即
,即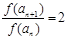
∴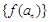 是以
是以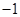 为首项,
为首项,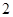 为公比的等比数列,∴
为公比的等比数列,∴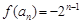 .……6分
.……6分
(III)由(II)得,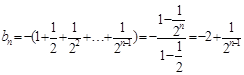 ……8分
……8分
∴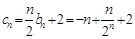 ,……9分
,……9分
则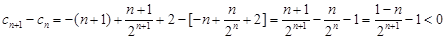
∴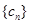 是递减数列,∴
是递减数列,∴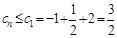 ,……10分
,……10分
要使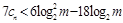 对任意
对任意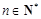 恒成立,
恒成立,
只需 ,即
,即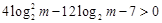 ,
,
故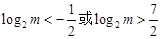 ,∴
,∴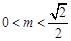 ,或
,或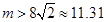 ,∴当
,∴当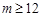 ,且
,且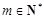 时,
时,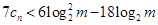 对任意
对任意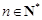 恒成立,∴
恒成立,∴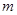 的最小正整数值为
的最小正整数值为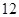 .…14分
.…14分
 ,∴
,∴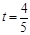 ……2分
……2分(II)
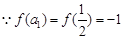 ,且
,且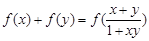
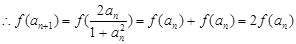 ,即
,即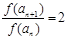
∴
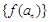 是以
是以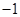 为首项,
为首项,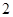 为公比的等比数列,∴
为公比的等比数列,∴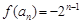 .……6分
.……6分(III)由(II)得,
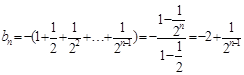 ……8分
……8分∴
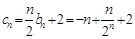 ,……9分
,……9分则
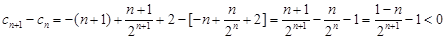
∴
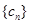 是递减数列,∴
是递减数列,∴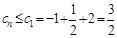 ,……10分
,……10分要使
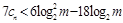 对任意
对任意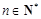 恒成立,
恒成立,只需
 ,即
,即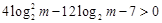 ,
,故
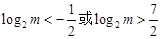 ,∴
,∴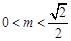 ,或
,或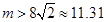 ,∴当
,∴当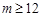 ,且
,且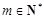 时,
时,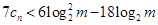 对任意
对任意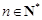 恒成立,∴
恒成立,∴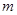 的最小正整数值为
的最小正整数值为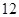 .…14分
.…14分略

