如果正数a,b,c,d满足a+b=cd=4,那么
- A.ab≤c+d且等号成立时a,b,c,d的取值唯一
- B.ab≥c+d且等号成立时a,b,c,d的取值唯一
- C.ab≤c+d且等号成立时a,b,c,d的取值不唯一
- D.ab≥c+d且等号成立时a,b,c,d的取值不唯一
A
分析:根据均值不等式分别有: ;
;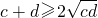 ;则a,b,c,d满足a+b=cd=4,进而可得2
;则a,b,c,d满足a+b=cd=4,进而可得2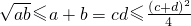
化简即得. 当且仅当a=b=c=d=2时取等号.
解答:如果a,b是正数,则根据均值不等式有: ,则(a+b)2≥4ab
,则(a+b)2≥4ab
如果c,d是正数,则根据均值不等式有: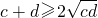 ; 则
; 则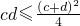
∵a,b,c,d满足a+b=cd=4,
∴2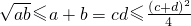
当且仅当a=b=c=d=2时取等号.
化简即为:ab≤c+d且等号成立时a,b,c,d的取值唯一.
故选A.
点评:要熟练使用均值不等式,能正用、逆用,而且还要会变用.使用时还要特别注意等号成立的条件.
分析:根据均值不等式分别有:
 ;
;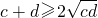 ;则a,b,c,d满足a+b=cd=4,进而可得2
;则a,b,c,d满足a+b=cd=4,进而可得2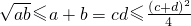
化简即得. 当且仅当a=b=c=d=2时取等号.
解答:如果a,b是正数,则根据均值不等式有:
 ,则(a+b)2≥4ab
,则(a+b)2≥4ab如果c,d是正数,则根据均值不等式有:
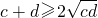 ; 则
; 则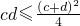
∵a,b,c,d满足a+b=cd=4,
∴2
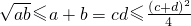
当且仅当a=b=c=d=2时取等号.
化简即为:ab≤c+d且等号成立时a,b,c,d的取值唯一.
故选A.
点评:要熟练使用均值不等式,能正用、逆用,而且还要会变用.使用时还要特别注意等号成立的条件.

