【题目】在边长为2的等边三角形中，点分别是边上的点，满足 且，（），将沿直线折到的位置.在翻折过程中，下列结论不成立的是（ ）

A.在边上存在点，使得在翻折过程中，满足平面

B.存在，使得在翻折过程中的某个位置，满足平面平面

C.若，当二面角为直二面角时，

D.在翻折过程中，四棱锥体积的最大值记为，的最大值为

【答案】ABC

【解析】

对于A.在边上点F，在上取一点N，使得，在上取一点H，使得，作交于点G，即可判断出结论.

对于B，，在翻折过程中，点在底面的射影不可能在交线上，即可判断出结论.

对于C，，当二面角为直二面角时，取ED的中点M，可得平面.可得，结合余弦定理即可得出.

对于D.在翻折过程中，取平面平面，四棱锥体积，，利用导数研究函数的单调性即可得出.

对于A.在边上点F，在上取一点N，使得，在上取一点H，使得，作交于点G，如图所示，

则可得平行且等于，即四边形为平行四边形，

∴，而始终与平面相交，

因此在边上不存在点F，使得在翻折过程中，满足平面，A不正确.

对于B，，在翻折过程中，点在底面的射影不可能在交线上，因此不满足平面平面，因此B不正确.

对于C.，当二面角为直二面角时，取的中点M，如图所示：

可得平面，

则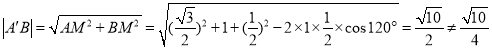，因此C不正确；

对于D.在翻折过程中，取平面AED⊥平面BCDE，四棱锥体积，，，可得时，函数取得最大值，因此D正确.

综上所述，不成立的为ABC.

故选：ABC.

关闭