【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)设函数![]() ,若存在
,若存在![]() ,对任意的
,对任意的![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(2)实数
;(2)实数![]() 的取值范围为
的取值范围为![]() .
.
【解析】
试题分析:(1)首先确定函数的定义域,进一步对![]() 求导,利用导函数与原函数的关系,得到原函数的单调区间;(2)“存在
求导,利用导函数与原函数的关系,得到原函数的单调区间;(2)“存在![]() ,对任意的
,对任意的![]() ,总有
,总有![]() 成立”等价于“
成立”等价于“![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() 在
在![]() 上的最大值”进一步,分别求函数
上的最大值”进一步,分别求函数![]() 和
和![]() 在区间
在区间![]() 和
和![]() 上的最大值.
上的最大值.
试题解析:(1) ![]() ,(此处若不写定义域,可适当扣分)
,(此处若不写定义域,可适当扣分)
故![]() .
.
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
![]()
![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;
;
(2)![]() ,则
,则![]() ,
,
而![]() ,故在
,故在![]() 上
上![]() ,即函数
,即函数![]() 在
在![]() 上单调递增,
上单调递增,![]()
![]()
而“存在![]() ,对任意的
,对任意的![]() ,总有
,总有![]() 成立”等价于“
成立”等价于“![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() 在
在![]() 上的最大值”
上的最大值”
而![]() 在
在![]() 上的最大值为
上的最大值为![]() 中的最大者,记为
中的最大者,记为![]() .
.
所以有![]() ,
,![]() ,
,
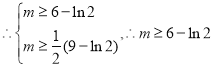 .
.
故实数![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
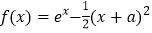 .
.(1)若曲线
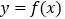 在点
在点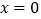 处的切线斜率为1,求函数
处的切线斜率为1,求函数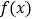 的单调区间;
的单调区间;(2)若
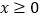 时,
时,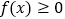 恒成立,求实数
恒成立,求实数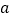 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】用n种不同的颜色为下列两块广告牌着色,(如图甲、乙),要求在A,B,C,D四个区域中相邻(有公共边界)的区域不用同一颜色.
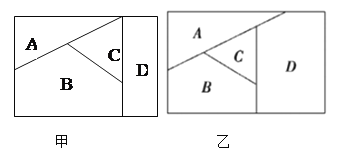
(1)若n=6,则为甲图着色时共有多少种不同的方法;
(2)若为乙图着色时共有120种不同方法,求n.
-
科目: 来源: 题型:
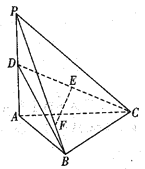
查看答案和解析>>【题目】如图,三棱锥
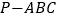 中,
中,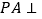 平面
平面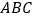 ,
,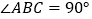 ,
,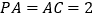 ,
,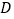 是
是 的中点,
的中点,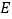 是
是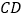 的中点,点
的中点,点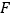 在
在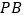 上,
上,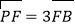 .
.
(1)证明:
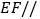 平面
平面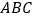 ;
;(2)若
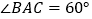 ,求点
,求点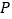 到平面
到平面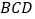 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】微信是现代生活中进行信息交流的重要工具.据统计,某公司200名员工中90%的人使用微信,其中每天使用微信时间在一小时以内的有60人,其余的员工每天使用微信时间在一小时以上,若将员工分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,那么使用微信的人中75%是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,那么经常使用微信的员工中都是青年人.
(1)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出并完成2×2列联表:

(2)由列联表中所得数据判断,是否有99.9%的把握认为“经常使用微信与年龄有关”?
(3)采用分层抽样的方法从“经常使用微信”的人中抽取6人,从这6人中任选2人,求选出的2人,均是青年人的概率.
附:

 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知各项均为正数的等比数列{an}中,a4与a14的等比中项为
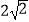 ,则2a7+a11的最小值为 .
,则2a7+a11的最小值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】若方程
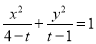 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:①若C为椭圆,则1<t<4且t≠
 ;
;②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆;
④若C表示椭圆,且长轴在x轴上,则1<t<
 .
.其中正确的命题是________(把所有正确命题的序号都填在横线上).
相关试题

