观察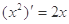 ,
,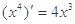 ,
,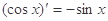 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在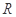 上的函数
上的函数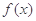 满足
满足 ,记
,记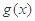 为
为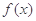 的导函数,则
的导函数,则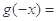 ( )
( )
A.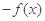 | B.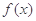 | C.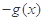 | D.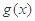 |
参考答案:
C
解析试题分析:观察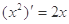 ,
,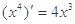 ,
,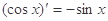 ,由归纳推理可得偶函数的导函数为奇函数,由
,由归纳推理可得偶函数的导函数为奇函数,由 可知函数
可知函数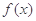 为偶函数,又
为偶函数,又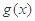 为
为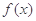 的导函数,所以为
的导函数,所以为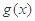 奇函数,因此
奇函数,因此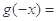
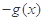 ,答案选C.
,答案选C.
考点:归纳推理与演绎推理
-
科目: 来源: 题型:单选题
查看答案和解析>>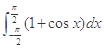 等于( )
等于( )A. 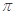
B.2 C. 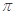 -2
-2D. 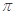 +2
+2 -
科目: 来源: 题型:单选题
查看答案和解析>>函数
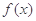 的定义域为开区间
的定义域为开区间 ,导函数
,导函数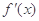 在
在 内的图象如图所示,则函数
内的图象如图所示,则函数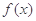 在开区间
在开区间 内有极小值点( )
内有极小值点( )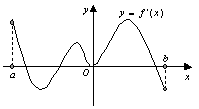
A. 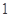 个
个 B.  个
个 C. 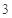 个
个 D.  个
个 -
科目: 来源: 题型:单选题
查看答案和解析>>若
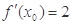 ,则
,则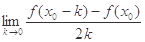 等于( )
等于( )A.-1 B.-2 C.1 D. 
-
科目: 来源: 题型:单选题
查看答案和解析>>已知函数
 的导函数为
的导函数为  ,满足
,满足  ,且
,且 ,则
,则 的单调性情况为
的单调性情况为
A.先增后减 B单调递增 C.单调递减 D先减后增 -
科目: 来源: 题型:单选题
查看答案和解析>>函数
 在
在 处的切线方程是( )
处的切线方程是( )A. 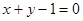
B. 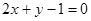
C. 
D. 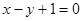
-
科目: 来源: 题型:单选题
查看答案和解析>>下列四个判断:
①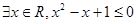 ;
;
②已知随机变量X服从正态分布N(3, ),P(X≤6)=0.72,则P(X≤0)=0.28;
),P(X≤6)=0.72,则P(X≤0)=0.28;
③已知 的展开式的各项系数和为32,则展开式中x项的系数为20;
的展开式的各项系数和为32,则展开式中x项的系数为20;
④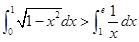
其中正确的个数有:A.1个 B.2个 C.3个 D.4个
相关试题

