【题目】如图，在直三棱柱中，，，，点E，F分别在，，且，.设.

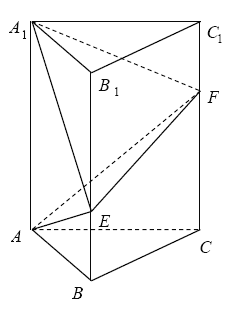
（1）当时，求异面直线与所成角的大小；

（2）当平面平面时，求的值.

【答案】（1）60°（2）

【解析】

（1）推导出平面ABC，AC，建立分别以AB，AC，为轴的空间直角坐标系，利用法向量能求出异面直线AE与所成角．
（2）推导出平面的法向量和平面的一个法向量，由平面平面，能求出的值．

解：因为直三棱柱，

所以平面，

因为平面，

所以，，

又因为，

所以建立分别以，，为轴的空间直角坐标系.

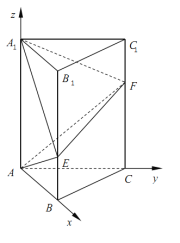
（1）设，则，，

各点的坐标为，，，.

，.

因为，，

所以.

所以向量和所成的角为120°，

所以异面直线与所成角为60°；

（2）因为，，

，

设平面的法向量为，

则，且.

即，且.

令，则，.

所以是平面的一个法向量.

同理，是平面的一个法向量.

因为平面平面，

所以，

，

解得.

所以当平面平面时，.

关闭