
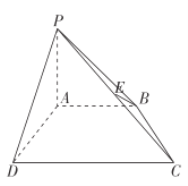
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明出四边形
,证明出四边形![]() 为平行四边形,可得出
为平行四边形,可得出![]() ,并推导出
,并推导出![]() 平面
平面![]() ,进而可得出
,进而可得出![]() 平面
平面![]() ;
;
(2)推导出![]() 平面
平面![]() ,可得知直线
,可得知直线![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,即为
的距离,即为![]() ,进而得解.
,进而得解.
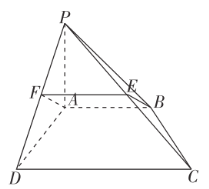
(1)如下图,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() .
.
又![]() 为
为![]() 的中点,则
的中点,则![]() 是
是![]() 的中位线,所以
的中位线,所以![]() 且
且![]() .
.
又![]() 且
且![]() ,所以
,所以![]() 且
且![]() .
.
所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() .
.
因为![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() ;
;
(2)因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
所以直线![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离.
的距离.
由(1)得![]() 平面
平面![]() ,则
,则![]() 等于点
等于点![]() 到平面
到平面![]() 的距离.
的距离.
因为![]() ,所以
,所以![]() .
.
故点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,即直线
,即直线![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,点![]() 、
、![]() ,点
,点![]() 是圆
是圆![]() 上一动点,线段
上一动点,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .且直线
.且直线![]() 交曲线
交曲线![]() 于
于![]() 两点(点
两点(点![]() 在
在![]() 轴的上方).
轴的上方).

(1)求曲线![]() 的方程;
的方程;
(2)试判断直线![]() 与曲线
与曲线![]() 的另一交点
的另一交点![]() 是否与点
是否与点![]() 关于
关于![]() 轴对称?
轴对称?
查看答案和解析>>
科目:高中数学 来源: 题型:
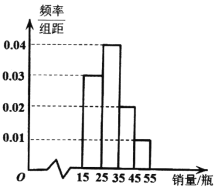
【题目】某早餐店对一款新口味的酸奶进行了一段时间试销,定价为![]() 元/瓶.酸奶在试销售期间足量供应,每天的销售数据按照
元/瓶.酸奶在试销售期间足量供应,每天的销售数据按照![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到如下频率分布直方图,以不同销量的频率估计概率.
分组,得到如下频率分布直方图,以不同销量的频率估计概率.
![]() 从试销售期间任选三天,求其中至少有一天的酸奶销量大于
从试销售期间任选三天,求其中至少有一天的酸奶销量大于![]() 瓶的概率;
瓶的概率;
![]() 试销结束后,这款酸奶正式上市,厂家只提供整箱批发:大箱每箱
试销结束后,这款酸奶正式上市,厂家只提供整箱批发:大箱每箱![]() 瓶,批发成本
瓶,批发成本![]() 元;小箱每箱
元;小箱每箱![]() 瓶,批发成本
瓶,批发成本![]() 元.由于酸奶保质期短,当天未卖出的只能作废.该早餐店以试销售期间的销量作为参考,决定每天仅批发一箱(计算时每个分组取中间值作为代表,比如销量为
元.由于酸奶保质期短,当天未卖出的只能作废.该早餐店以试销售期间的销量作为参考,决定每天仅批发一箱(计算时每个分组取中间值作为代表,比如销量为![]() 时看作销量为
时看作销量为![]() 瓶).
瓶).
①设早餐店批发一大箱时,当天这款酸奶的利润为随机变量![]() ,批发一小箱时,当天这款酸奶的利润为随机变量
,批发一小箱时,当天这款酸奶的利润为随机变量![]() ,求
,求![]() 和
和![]() 的分布列和数学期望;
的分布列和数学期望;
②以利润作为决策依据,该早餐店应每天批发一大箱还是一小箱?
注:销售额=销量×定价;利润=销售额-批发成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() ,
,![]() 为左、右焦点,
为左、右焦点,![]() 为短轴端点,且
为短轴端点,且![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程,
的方程,
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆C恒有两个交点![]() ,
,![]() ,且满足
,且满足![]() ?若存在,求出该圆的方程,若不存在,说明理由.
?若存在,求出该圆的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十二生肖,又称十二属相,中国古人拿十二种动物来配十二地支,组成子鼠、丑牛、寅虎、卯兔、辰龙、已蛇、午马、未羊、申猴、西鸡、戌狗、亥猪十二属相现有十二生肖吉祥物各一件,甲、乙、丙三位同学依次随机抽取一件作为礼物,甲同学喜欢马、牛,乙同学喜欢马、龙、狗,丙同学除了鼠不喜欢外其他的都喜欢,则这三位同学抽取的礼物都喜欢的概率是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
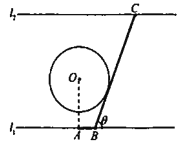
【题目】如图为某大江的一段支流,岸线![]() 与
与![]() 近似满足
近似满足![]() ∥
∥![]() ,宽度为
,宽度为![]() .圆
.圆![]() 为江中的一个半径为
为江中的一个半径为![]() 的小岛,小镇
的小岛,小镇![]() 位于岸线
位于岸线![]() 上,且满足岸线
上,且满足岸线![]() ,
,![]() .现计划建造一条自小镇
.现计划建造一条自小镇![]() 经小岛
经小岛![]() 至对岸
至对岸![]() 的水上通道
的水上通道![]() (图中粗线部分折线段,
(图中粗线部分折线段,![]() 在
在![]() 右侧),为保护小岛,
右侧),为保护小岛,![]() 段设计成与圆
段设计成与圆![]() 相切.设
相切.设![]() .
.
(1)试将通道![]() 的长
的长![]() 表示成
表示成![]() 的函数,并指出定义域;
的函数,并指出定义域;
(2)若建造通道的费用是每公里100万元,则建造此通道最少需要多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车尾气中含有一氧化碳(![]() ),碳氢化合物(
),碳氢化合物(![]() )等污染物,是环境污染的主要因素之一,汽车在使用若干年之后排放的尾气中的污染物会出现递增的现象,所以国家根据机动车使用和安全技术、排放检验状况,对达到报废标准的机动车实施强制报废.某环保组织为了解公众对机动车强制报废标准的了解情况,随机调查了100人,所得数据制成如下列联表:
)等污染物,是环境污染的主要因素之一,汽车在使用若干年之后排放的尾气中的污染物会出现递增的现象,所以国家根据机动车使用和安全技术、排放检验状况,对达到报废标准的机动车实施强制报废.某环保组织为了解公众对机动车强制报废标准的了解情况,随机调查了100人,所得数据制成如下列联表:
不了解 | 了解 | 总计 | |
女性 |
|
| 50 |
男性 | 15 | 35 | 50 |
总计 |
|
| 100 |
(1)若从这100人中任选1人,选到了解机动车强制报废标准的人的概率为![]() ,问是否有
,问是否有![]() 的把握认为“对机动车强制报废标准是否了解与性别有关”?
的把握认为“对机动车强制报废标准是否了解与性别有关”?
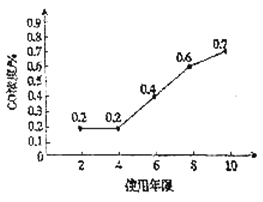
(2)该环保组织从相关部门获得某型号汽车的使用年限与排放的尾气中![]() 浓度的数据,并制成如图所示的折线图,若该型号汽车的使用年限不超过15年,可近似认为排放的尾气中
浓度的数据,并制成如图所示的折线图,若该型号汽车的使用年限不超过15年,可近似认为排放的尾气中![]() 浓度
浓度![]() 与使用年限
与使用年限![]() 线性相关,试确定
线性相关,试确定![]() 关于
关于![]() 的回归方程,并预测该型号的汽车使用12年排放尾气中的
的回归方程,并预测该型号的汽车使用12年排放尾气中的![]() 浓度是使用4年的多少倍.
浓度是使用4年的多少倍.
附: (
(![]() )
)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:用最小二乘法求线性回归方程系数公式: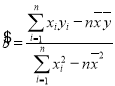 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了了解该企业工人组装某产品所用时间,对每个工人组装一个该产品的用时作了记录,得到大量统计数据.从这些统计数据中随机抽取了![]() 个数据作为样本,得到如图所示的茎叶图(单位:分钟).若用时不超过
个数据作为样本,得到如图所示的茎叶图(单位:分钟).若用时不超过![]() (分钟),则称这个工人为优秀员工.
(分钟),则称这个工人为优秀员工.
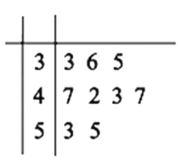
(1)求这个样本数据的中位数和众数;
(2)以这![]() 个样本数据中优秀员工的频率作为概率,任意调查
个样本数据中优秀员工的频率作为概率,任意调查![]() 名工人,求被调查的
名工人,求被调查的![]() 名工人中优秀员工的数量
名工人中优秀员工的数量![]() 分布列和数学期望.
分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com