
【题目】已知函数![]() 为奇函数,且
为奇函数,且![]() 的极小值为
的极小值为![]() .
.
(Ⅰ)求![]() 和
和![]() 的值;
的值;
(Ⅱ)若过点![]() 可作三条不同的直线与曲线
可作三条不同的直线与曲线![]() 相切,求实数
相切,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ,
,![]() .(Ⅱ)
.(Ⅱ)![]()
【解析】
(Ⅰ)根据题意可得![]() ,代入表达式可得
,代入表达式可得![]() ,从而可得
,从而可得![]() ,求导函数令
,求导函数令![]() ,求出极值点,再利用导数判断函数的单调性,进而确定
,求出极值点,再利用导数判断函数的单调性,进而确定![]() 的极小值为
的极小值为![]() ,由
,由![]() 即可求解.
即可求解.
(Ⅱ)由(Ⅰ)可知![]() ,设点
,设点![]() 是曲线
是曲线![]() 的切点,利用导数的几何意义求出切线方程,将点
的切点,利用导数的几何意义求出切线方程,将点![]() 代入切线方程得
代入切线方程得![]() ,设
,设![]() ,只要使函数
,只要使函数![]() 有3个零点即可,利用导数与函数单调性的关系可得
有3个零点即可,利用导数与函数单调性的关系可得![]() ,解不等式组即可.
,解不等式组即可.
(Ⅰ)因为![]() 是奇函数,所以
是奇函数,所以![]() 恒成立,则
恒成立,则![]() .
.
所以![]() ,所以
,所以![]() ,
,
则![]()
令![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,所以
单调递增,所以![]() 的极小值为
的极小值为![]() ,
,
由![]() ,解得
,解得![]() ,
,
所以![]() ,
,![]() .
.
(Ⅱ)由(Ⅰ)可知![]() ,
,
设点![]() 是曲线
是曲线![]() 的切点,则在
的切点,则在![]() 点处的切线的方程为
点处的切线的方程为![]() 即
即![]()
因为其过点![]() ,所以,
,所以,![]() ,
,
由于有三条切线,所以方程应有3个实根,
设![]() ,只要使曲线
,只要使曲线![]() 有3个零点即可.
有3个零点即可.
设![]() ,∴
,∴![]() 或
或![]() 分别为
分别为![]() 的极值点,
的极值点,
当![]() 和
和![]() 时
时![]() ,
,![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,
当![]() 时
时![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
所以,![]() 为极大值点,
为极大值点,![]() 为极小值点.
为极小值点.
所以要使曲线![]() 与
与![]() 轴有3个交点,当且仅当
轴有3个交点,当且仅当![]() ,即
,即![]() ,
,
解得![]() .
.
即实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
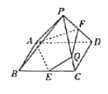
【题目】如图,在底面为菱形的四棱锥P-ABCD中,平面![]() 平面ABCD,
平面ABCD,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,点E,F分别为BC,PD的中点,直线PC与平面AEF交于点Q.
,点E,F分别为BC,PD的中点,直线PC与平面AEF交于点Q.
(1)若平面![]() 平面
平面![]() ,求证:
,求证:![]() .
.
(2)求直线AQ与平面PCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在一次期末数学测试中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于65分到145分之间(满分150分),将统计结果按如下方式分成八组:第一组![]() ,
,![]() ,第二组
,第二组![]() ,
,![]() ,
,![]() 第八组
第八组![]() ,
,![]() ,如图是按上述分组方法得到的频率分布直方图的一部分.
,如图是按上述分组方法得到的频率分布直方图的一部分.
(1)求第七组的频率,并完成频率分布直方图;
(2)用样本数据估计该校的2000名学生这次考试成绩的平均分(同一组中的数据用该组区间的中点值代表该组数据平均值);
(3)若从样本成绩属于第六组和第八组的所有学生中随机抽取2名,求他们的分差的绝对值小于10分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的角A、B、C的对边分别为a、b、c,![]() =(2b-c,a),
=(2b-c,a),![]() =(cosA,-cosC),且
=(cosA,-cosC),且![]() ⊥
⊥![]() .
.
(Ⅰ)求角A的大小;
(Ⅱ)当y=2sin2B+sin(2B+![]() )取最大值时,求角
)取最大值时,求角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆锥![]() (其中
(其中![]() 为顶点,
为顶点,![]() 为底面圆心)的侧面积与底面积的比是
为底面圆心)的侧面积与底面积的比是![]() ,则圆锥
,则圆锥![]() 与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )
与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系![]() 中,曲线
中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,设
,设![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 中点为
中点为![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() 、
、![]() .以
.以![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴的正半轴建立直角坐标系
轴的正半轴建立直角坐标系![]() .
.
(1)求![]() 的直角坐标方程与点
的直角坐标方程与点![]() 的直角坐标;
的直角坐标;
(2)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某印刷厂为了研究单册书籍的成本![]() (单位:元)与印刷册数
(单位:元)与印刷册数![]() (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
印刷册数 |
|
|
|
|
|
单册成本 |
|
|
|
|
|
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到![]() );
);
印刷册数 |
|
|
|
|
| |
单册成本 |
|
|
|
|
| |
模型甲 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
模型乙 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
②分别计算模型甲与模型乙的残差平方和,并通过比较,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷,根据市场调查,新需求量为![]() 千册,若印刷厂以每册
千册,若印刷厂以每册![]() 元的价格将书籍出售给订货商,求印刷厂二次印刷
元的价格将书籍出售给订货商,求印刷厂二次印刷![]() 千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com