【题目】坐标系与参数方程:在平面直角坐标系中,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,已知点
轴的非负半轴为极轴建立极坐标系,已知点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且点
,且点![]() 在直线
在直线![]() 上
上
(Ⅰ)求![]() 的值和直线
的值和直线![]() 的直角坐标方程及
的直角坐标方程及![]() 的参数方程;
的参数方程;
(Ⅱ)已知曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),直线
为参数),直线![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
【答案】(Ⅰ)![]() ,
,![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,![]() 的参数方程为:
的参数方程为: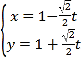 (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)将点![]() 的极坐标方程代入直线
的极坐标方程代入直线![]() 的极坐标方程可求出
的极坐标方程可求出![]() 的值,然后将直线
的值,然后将直线![]() 方程化为普通方程,确定直线
方程化为普通方程,确定直线![]() 的倾斜角,即可将直线
的倾斜角,即可将直线![]() 的方程表示为参数方程的形式;
的方程表示为参数方程的形式;
(Ⅱ)将曲线![]() 的参数方程表示普通方程,然后将(Ⅰ)中直线
的参数方程表示普通方程,然后将(Ⅰ)中直线![]() 的参数方程与曲线
的参数方程与曲线![]() 的普通方程联立,得到关于
的普通方程联立,得到关于![]() 的一元二次方程,并列出韦达定理,根据
的一元二次方程,并列出韦达定理,根据![]() 的几何意义计算出
的几何意义计算出
![]() 和
和![]() ,于是可得出
,于是可得出
![]() 的值。
的值。
解:(Ⅰ)因为点![]() ,所以
,所以![]() ;
;
由![]() 得
得![]()
于是![]() 的直角坐标方程为
的直角坐标方程为![]() ;
;
![]() 的参数方程为:
的参数方程为: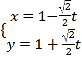 (t为参数)
(t为参数)
(Ⅱ)由![]() :
:![]()
![]()
![]() ,
,
将![]() 的参数方程代入
的参数方程代入![]() 得
得
![]() ,设该方程的两根为
,设该方程的两根为![]() ,由直线
,由直线![]() 的参数
的参数![]() 的几何意义及曲线
的几何意义及曲线![]() 知,
知,
![]() ,
,
![]()
所以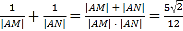 。
。

