【题目】在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系，已知直线l的参数方程为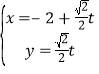：，为参数点的极坐标为，曲线C的极坐标方程为．

Ⅰ试将曲线C的极坐标方程化为直角坐标方程，并求曲线C的焦点在直角坐标系下的坐标；

Ⅱ设直线l与曲线C相交于两点A，B，点M为AB的中点，求的值．

【答案】（Ⅰ）曲线C的直角坐标方程为，焦点坐标为；（Ⅱ）．

【解析】

Ⅰ把，代入曲线C的方程，可得曲线C的直角坐标方程．Ⅱ设点A，B，M对应的参数为，，，由题意可知把直线l的参数方程代入抛物线的直角坐标方程，利用韦达定理求得的值，可得的值．

解：Ⅰ把，代入，可得曲线C的直角坐标方程为，

它是开口向上的抛物线，焦点坐标为．

Ⅱ点P的直角坐标为，它在直线l上，在直线l的参数方程中，

设点A，B，M对应的参数为，，，由题意可知．

把直线l的参数方程代入抛物线的直角坐标方程，得．

因为，

所以．

关闭