【题目】关于函数![]() 有如下四个结论:
有如下四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 在区间
在区间![]() 上单调递增;③
上单调递增;③![]() 最大值为
最大值为![]() ;④
;④![]() 在
在![]() 上有四个零点,其中正确命题的序号是_______.
上有四个零点,其中正确命题的序号是_______.
参考答案:
【答案】①③
【解析】
利用奇偶性的定义判定函数![]() 的奇偶性,可判断出命题①的正误;在
的奇偶性,可判断出命题①的正误;在![]() 时,去绝对值,化简函数
时,去绝对值,化简函数![]() 的解析式,可判断函数
的解析式,可判断函数![]() 在区间
在区间![]() 上的单调性,可判断命题②的正误;由
上的单调性,可判断命题②的正误;由![]() 以及
以及![]() 可判断出命题③的正误;化简函数
可判断出命题③的正误;化简函数![]() 在区间
在区间![]() 上的解析式,求出该函数的零点,即可判断命题④的正误.
上的解析式,求出该函数的零点,即可判断命题④的正误.
对于命题①,函数![]() 的定义域为
的定义域为![]() ,关于原点对称,
,关于原点对称,
且![]() ,该函数为偶函数,命题①正确;
,该函数为偶函数,命题①正确;
对于命题②,当![]() 时,
时,![]() ,则
,则![]() ,则函数
,则函数![]() 在
在![]() 上单调递减,命题②错误;
上单调递减,命题②错误;
对于命题③,![]() ,
,![]() ,
,![]() ,又
,又![]() ,所以,函数
,所以,函数![]() 的最大值为
的最大值为![]() ,命题③正确;
,命题③正确;
对于命题④,当![]() 时,
时,![]() ,
,![]() ,
,
由于该函数为偶函数,当![]() 时,
时,![]() ,
,
又![]() ,所以,该函数在区间
,所以,该函数在区间![]() 上有且只有三个零点.
上有且只有三个零点.
因此,正确命题的序号为①③.
故答案为:①③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 为等边三角形,
为等边三角形, 分别为
分别为 的中点,
的中点, 为
为 的中点,
的中点, ,将
,将 沿
沿 折起到
折起到 的位置,使得平面
的位置,使得平面 平面
平面 ,
,
为
 的中点,如图2.
的中点,如图2.
(1)求证:
 平面
平面 ;
;(2)求点
 到平面
到平面 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
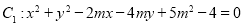 ,圆
,圆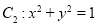
(1)若圆
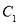 、
、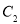 相交,求
相交,求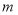 的取值范围;
的取值范围;(2)若圆
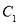 与直线
与直线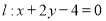 相交于
相交于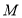 、
、 两点,且
两点,且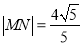 ,求
,求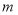 的值;
的值;(3)已知点
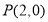 ,圆
,圆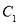 上一点
上一点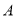 ,圆
,圆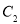 上一点
上一点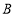 ,求
,求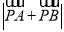 的最小值的取值范围.
的最小值的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前
的前 项和为
项和为 ,
,  ,
,  .等 差数列
.等 差数列 中,
中,  ,且公差
,且公差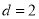 .
.(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)是否存在正整数
 ,使得
,使得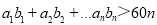 ?.若存在,求出
?.若存在,求出 的最小值;若 不存在,请说明理由.
的最小值;若 不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
 的极坐标方程是
的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 (
( 为参数).
为参数).(Ⅰ)将曲线
 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;(Ⅱ)若直线
 与曲线
与曲线 相交于
相交于 ,
,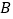 两点,且
两点,且 ,求直线
,求直线 的倾斜角
的倾斜角 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
第
 天
天1
2
3
4
5
被感染的计算机数量
 (台)
(台)10
20
39
81
160
则下列函数模型中,能较好地反映计算机在第
 天被感染的数量
天被感染的数量 与
与 之间的关系的是
之间的关系的是A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数
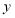 与听课时间
与听课时间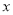 (单位:分钟)之间的关系满足如图所示的图象,当
(单位:分钟)之间的关系满足如图所示的图象,当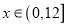 时,图象是二次函数图象的一部分,其中顶点
时,图象是二次函数图象的一部分,其中顶点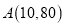 ,过点
,过点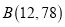 ;当
;当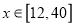 时,图象是线段
时,图象是线段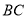 ,其中
,其中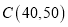 .根据专家研究,当注意力指数大于62时,学习效果最佳.
.根据专家研究,当注意力指数大于62时,学习效果最佳.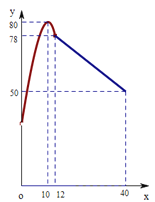
(Ⅰ)试求
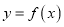 的函数关系式;
的函数关系式;(Ⅱ)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
相关试题

