【题目】设函数![]()
![]() ,且
,且![]() 为
为![]() 的极值点.
的极值点.
(Ⅰ) 若![]() 为
为![]() 的极大值点,求
的极大值点,求![]() 的单调区间(用
的单调区间(用![]() 表示);
表示);
(Ⅱ)若![]() 恰有1解,求实数
恰有1解,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】![]()
因为![]() 为
为![]() 的极值点,所以
的极值点,所以![]()
所以![]() 且
且![]() ,
,![]() ……………3分
……………3分
(1)因为![]() 为
为![]() 的极大值点,所以
的极大值点,所以![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
所以![]() 的递增区间为
的递增区间为![]() ,
,![]() ;递减区间为
;递减区间为![]() .…………6分
.…………6分
(2)若![]() ,则
,则![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增
![]() 恰有1解,则
恰有1解,则![]() ,即
,即![]() ,所以
,所以![]() ;…………9分
;…………9分
若![]() ,则
,则![]() ,
,![]()
因为![]() ,则
,则![]()
![]() ,从而
,从而![]() 恰有一解; ……………12分
恰有一解; ……………12分
若![]() ,则
,则![]()
![]() ,从而
,从而![]() 恰有一解;
恰有一解;
所以所求![]() 的范围为
的范围为![]() .
.
【解析】
(1)由![]() ,知
,知![]() ,由x=1为f(x)的极值点,知
,由x=1为f(x)的极值点,知![]() .由x=1为f(x)的极大值点,知c>1.由此能求出f(x)的单调区间.
.由x=1为f(x)的极大值点,知c>1.由此能求出f(x)的单调区间.
( II)若c<0,则f(x)在(0,1)上递减,在(1,+∞)上递增f(x)=0恰有1解,则f(1)=0,实数c的取值范围.
![]() ,又
,又![]() ,
,
则![]() ,所以
,所以![]() 且
且![]() .
.
(1)因为![]() 为
为![]() )的极大值点,所以
)的极大值点,所以![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ;单调递减区间为
;单调递减区间为![]() .
.
(2)①若![]() ,则
,则![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() 恰有两解,则
恰有两解,则![]() ,则
,则![]() ,
,
所以![]() ;
;
②若![]() ,则
,则![]() ,
,![]() ,
,
因为![]() ,则
,则![]() ,
,
![]() ,从而
,从而![]() 只有一解;
只有一解;
③若![]() ,则
,则![]() ,
,
![]() ,则
,则![]() 只有一解.
只有一解.
综上,使![]() 恰有两解的
恰有两解的![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设直线
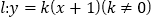 与椭圆
与椭圆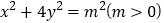 相交于
相交于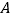 ,
,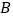 两个不同的点,与
两个不同的点,与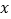 轴相交于点
轴相交于点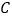 ,
, 为坐标原点.
为坐标原点.(1)证明:
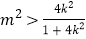 ;
;(2)若
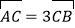 ,求
,求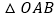 的面积取得最大值时椭圆的方程.
的面积取得最大值时椭圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图像经过点
的图像经过点 ,且满足
,且满足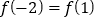 ,
,(1)求
 的解析式;
的解析式;(2)已知
 ,求函数
,求函数 在
在 的最大值和最小值;
的最大值和最小值;函数
 的图像上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由
的图像上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图(如图)和B地区用户满意度评分的频数分布表.

B地区用户满意度评分的频数分布表
满意度评分分组





频数
2
8
14
10
6
在图中作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
 的分组
的分组




企业数
2
24
53
14
7
(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;
(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01)
附:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}中的项按顺序可以排成如图的形式,第一行1项,排a1;第二行2项,从左到右分别排a2,a3;第三行3项,……依此类推,设数列{an}的前n项和为Sn,则满足Sn>2019的最小正整数n的值为()

A. 20B. 21C. 26D. 27
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用
水量







频数
1
3
2
4
9
26
5
使用了节水龙头50天的日用水量频数分布表
日用
水量






频数
1
5
13
10
16
5
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:

(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
相关试题

