【题目】己知函数，，.

（1）讨论函数的单调性；

（2）若在处取得极大值，求的取值范围.

【答案】(1) 在上是递增的，在上是递减的.(2) .

【解析】

(1)首先求得导函数的解析式，然后结合函数的定义域分类讨论函数的单调性即可；

(2)由题意结合(1)的结论可知，据此结合导函数的解析式分类讨论即可确定实数a的取值范围.

（1）∵

∴

∵

①当时， ∴在上是递增的

②当时，若，则，若，则

∴在上是递增的，在上是递减的.

（2）∵，∴

由（1）知：

①当时，在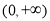上是递增的，

若，则，若，则

∴在取得极小值，不合题意

②时，在上是递增的，在上是递减的，

∴ ∴在上是递减的

∴无极值，不合题意.

③当时，，由（1）知: 在上是递增的，

∵

∴若，则，若，则，

∴在处取得极小值，不合题意.

④当时，，由（1）知: 在上是递减的，

∵

∴若，则，若），则，

∴在上是递增的，在上是递减的，

故在处取得极大值，符合题意.

综上所述:.

关闭