【题目】已知数列![]() 满足
满足![]() .
.
(1)若![]() (
(![]() 且
且![]() ),数列
),数列![]() 为递增数列,求数列
为递增数列,求数列![]() 的通项公式;
的通项公式;
(2)若![]() (
(![]() 且
且![]() ),数列
),数列![]() 为递增数列,数列
为递增数列,数列![]() 为递减数列,且
为递减数列,且![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
参考答案:
【答案】(1)![]() ;(2)
;(2)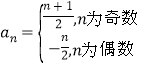 .
.
【解析】分析:(1)因为数列![]() 为递增数列,故可得
为递增数列,故可得![]() ,转化为
,转化为![]() ,结合
,结合![]() ,可得数列
,可得数列![]() 是首项
是首项![]() ,公差为1的等差数列,进而可得结果;(2)利用和(1)前半部分相同的思想可得
,公差为1的等差数列,进而可得结果;(2)利用和(1)前半部分相同的思想可得![]() 和
和![]() 成立,紧接着分为
成立,紧接着分为![]() 为奇数或者
为奇数或者![]() 为偶数即可.
为偶数即可.
详解:(1)因为数列![]() 为递增数列,所以
为递增数列,所以![]() ,即
,即![]() ,
,
![]() ,由条件,
,由条件,![]() ,
,
所以![]() ,
,
即数列![]() 是首项
是首项![]() ,公差为1的等差数列,
,公差为1的等差数列,
则![]() .
.
(2)因为数列![]() 为递增数列,
为递增数列,
所以![]() ,即
,即![]() ,
,
![]() ,由条件
,由条件![]() ,
,
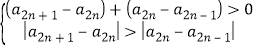 ,
,
得![]() (绝对值大的必为正数),
(绝对值大的必为正数),![]() ,
,
同理,数列![]() 为递减数列,所以
为递减数列,所以![]() ,即
,即![]() ,
,
![]() ,由条件,
,由条件,
![]() ,
,
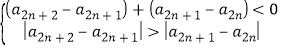 ,
,
得![]() (绝对值大的必为负数),
(绝对值大的必为负数),![]() ,
,
而![]() ,则
,则![]() ,
,
综上可知,当![]() 为奇数且
为奇数且![]() 时,
时,![]() ;
;
当![]() 为偶数时,
为偶数时,![]() .
.
当![]() 为奇数且
为奇数且![]() 时,
时,
![]()
![]()
![]() ,
,
当![]() 时,
时,![]() 也成立,
也成立,
即当![]() 为奇数时,
为奇数时,![]() ,
,
当![]() 为偶数时,
为偶数时,![]() 为奇数,
为奇数,![]() ,
,
所以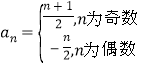 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
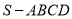 中,平面
中,平面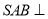 平面
平面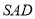 ,侧面
,侧面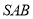 是边长为
是边长为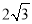 的等边三角形,底面
的等边三角形,底面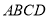 是矩形,且
是矩形,且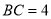 ,则该四棱锥外接球的表面积等于__________.
,则该四棱锥外接球的表面积等于__________. -
科目: 来源: 题型:
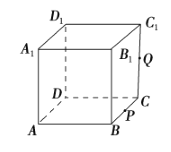
查看答案和解析>>【题目】如图,正方体
 的棱长为 1,
的棱长为 1,  为
为 的中点,
的中点,  为线段
为线段 上的动点,过点A、P、Q的平面截该正方体所得的截面记为
上的动点,过点A、P、Q的平面截该正方体所得的截面记为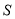 .则下列命题正确的是__________(写出所有正确命题的编号).
.则下列命题正确的是__________(写出所有正确命题的编号).①当
 时,
时, 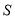 为四边形;②当
为四边形;②当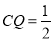 时,
时,  为等腰梯形;③当
为等腰梯形;③当 时,
时, 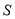 为六边形;④当
为六边形;④当 时,
时,  的面积为
的面积为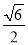 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,
在此几何体中,给出下面四个结论:
①直线BE与直线CF异面; ②直线BE与直线AF异面;
③直线EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正确的有( )
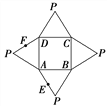
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正四棱锥P﹣ABCD中,PA=AB=2,点M,N分别在PA,BD上,且
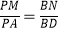 =
=  .
. 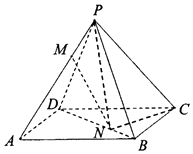
(1)求异面直线MN与PC所成角的大小;
(2)求二面角N﹣PC﹣B的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,平面
中,平面 平面
平面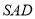 ,侧面
,侧面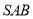 是边长为
是边长为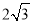 的等边三角形,底面
的等边三角形,底面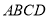 是矩形,且
是矩形,且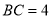 ,则该四棱锥外接球的表面积等于__________.
,则该四棱锥外接球的表面积等于__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一辆汽车从
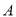 市出发沿海岸一条直公路以
市出发沿海岸一条直公路以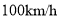 的速度向东匀速行驶,汽车开动时,在
的速度向东匀速行驶,汽车开动时,在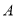 市南偏东30°方向距
市南偏东30°方向距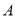 市
市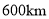 的海上
的海上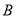 处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.问快艇至少以多大的速度,以什么样的航向行驶才能最快把稿件送到司机手中?
处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.问快艇至少以多大的速度,以什么样的航向行驶才能最快把稿件送到司机手中?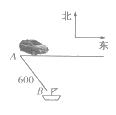
相关试题

