【题目】已知正实数a,b,c,函数f(x)=|x+a||x+b|. (Ⅰ)若a=1,b=3,解关于x的不等式f(x)+x+1<0;
(Ⅱ)求证:f(1)f(c)≥16abc.
参考答案:
【答案】解:(Ⅰ)原不等式等价于|(x+1)(x+3)|<﹣x﹣1x+1<(x+1)(x+3)<﹣x﹣1(2分) 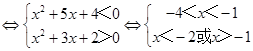
x∈(﹣4,﹣2),
∴解集为(﹣4,﹣2)
(Ⅱ)∵a,b,c为正数,
所以有 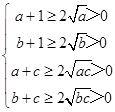
∴ ![]()
【解析】(Ⅰ)原不等式等价于|(x+1)(x+3)|<﹣x﹣1x+1<(x+1)(x+3)<﹣x﹣1,即可得出结论;(Ⅱ)利用基本不等式与不等式的性质证明f(1)f(c)≥16abc.
【考点精析】认真审题,首先需要了解绝对值不等式的解法(含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号),还要掌握不等式的证明(不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=ex与g(x)=ax+b的图象交于P(x1 , y1),Q(x2 , y2)两点. (Ⅰ)求函数h(x)=f(x)﹣g(x)的最小值;
(Ⅱ)且PQ的中点为M(x0 , y0),求证:f(x0)<a<y0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C的参数方程为
 ,在同一平面直角坐标系中,将曲线C上的点按坐标变换
,在同一平面直角坐标系中,将曲线C上的点按坐标变换  得到曲线C',以原点为极点,x轴的正半轴为极轴,建立极坐标系. (Ⅰ)求曲线C'的极坐标方程;
得到曲线C',以原点为极点,x轴的正半轴为极轴,建立极坐标系. (Ⅰ)求曲线C'的极坐标方程;
(Ⅱ)若过点 (极坐标)且倾斜角为
(极坐标)且倾斜角为  的直线l与曲线C'交于M,N两点,弦MN的中点为P,求
的直线l与曲线C'交于M,N两点,弦MN的中点为P,求  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数是同一函数的是( )
A.
 与
与 B.
B. 与
与
C.
 与
与 D.
D. 与
与
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋中有除颜色外完全相同的红、黄、白三种颜色的球各一个,从中每次任取1个.有放回地抽取3次,求:
(1)3个全是红球的概率. (2)3个颜色全相同的概率.
(3)3个颜色不全相同的概率. (4)3个颜色全不相同的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面命题正确的是( )
A.“
 ”是“
”是“ ”的 充 分不 必 要条件
”的 充 分不 必 要条件B.命题“若
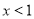 ,则
,则 ”的 否 定 是“ 存 在
”的 否 定 是“ 存 在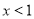 ,则
,则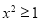 ”.
”.C.设
 ,则“
,则“ 且
且 ”是“
”是“ ”的必要而不充分条件
”的必要而不充分条件D.设
 ,则“
,则“ ”是“
”是“ ”的必要 不 充 分 条件
”的必要 不 充 分 条件 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中
(1)当
 时,求函数
时,求函数 在
在 上的值域;
上的值域;(2)若函数
 在
在 上的最小值为3,求实数
上的最小值为3,求实数 的取值范围.
的取值范围.
相关试题

