【题目】如图,甲船以每小时 ![]() 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距 ![]() 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里? 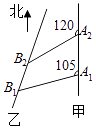
参考答案:
【答案】解:由题意可知A1B1=20,A2B2=10 ![]() ,A1A2=30
,A1A2=30 ![]() ×
× ![]() =10
=10 ![]() ,∠B2A2A1=180°﹣120°=60°, 连结A1B2 , 则△A1A2B2是等边三角形,
,∠B2A2A1=180°﹣120°=60°, 连结A1B2 , 则△A1A2B2是等边三角形,
∴A1B2=10 ![]() ,∠A2A1B2=60°.
,∠A2A1B2=60°.
∴∠B1A1B2=105°﹣60°=45°,
在△B1A1B2中,由余弦定理得B1B22=A1B12+A1B22﹣2A1B1A1B2cos∠B1A1B2=400+200﹣400=200.
∴B1B2=10 ![]() .
.
∴乙船的航行速度是 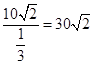 海里/小时.
海里/小时.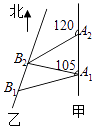
【解析】连结A1B2 , 则△A1A2B2是等边三角形,从而∠B1A1B2=105°﹣60°=45°,A1B2=10 ![]() ,在△B1A1B2中,由余弦定理求出B1B2得出乙船的速度.
,在△B1A1B2中,由余弦定理求出B1B2得出乙船的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
有甲、乙、丙、丁四名网球运动员,通过对过去战绩的统计,在一场比赛中,甲对乙、丙、丁取胜的概率分别为
 .
. (Ⅰ)若甲和乙之间进行三场比赛,求甲恰好胜两场的概率;
(Ⅱ)若四名运动员每两人之间进行一场比赛,设甲获胜场次为
 ,求随机变量
,求随机变量 的分布列及期望
的分布列及期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是递增的等差数列,它的前三项的和为﹣3,前三项的积为8.
(1)求数列{an}的通项公式;
(2)求数列{|an|}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是等差数列,
是等差数列, 是等比数列,且
是等比数列,且 ,则下列结论正确的是( )
,则下列结论正确的是( )A.
 B.
B. 
C.
 D.
D.  ,使得
,使得
-
科目: 来源: 题型:
查看答案和解析>>【题目】某金匠以黄金为原材料加工一种饰品,经多年的数据统计得知,该金匠平均每加5 个饰品中有4个成品和1个废品,每个成品可获利3万元,每个废品损失1万元,假设该金匠加工每件饰品互不影响,以频率估计概率.
(1)若金金匠加工4个饰品,求其中废品的数量不超过1的概率;
(2)若该金匠加工了 3个饰品,求他所获利润的数学期望.
(两小问的计算结果都用分数表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知在锐角△ABC中,角A,B,C所对的边分别为a,b,c,且tanC=
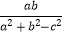 . (Ⅰ)求角C大小;
. (Ⅰ)求角C大小;
(Ⅱ)当c=1时,求ab的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
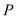 是圆
是圆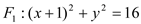 上任意一点,点
上任意一点,点 的坐标为
的坐标为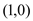 ,直线
,直线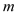 分别与线段
分别与线段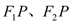 交于
交于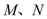 两点,且
两点,且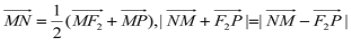 .
.(1)求点
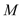 的轨迹
的轨迹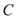 的方程;
的方程;(2)直线
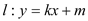 与轨迹
与轨迹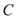 相交于
相交于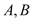 两点,设
两点,设 为坐标原点,
为坐标原点, 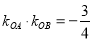 ,判断
,判断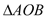 的面积是否为定值?若是,求出定值,若不是,说明理由.
的面积是否为定值?若是,求出定值,若不是,说明理由.
相关试题

