【题目】选修4-4:坐标系与参数方程
已知圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).若直线
为参数).若直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)写出圆![]() 的直角坐标方程,并求圆心的坐标与半径;
的直角坐标方程,并求圆心的坐标与半径;
(2)若弦长![]() ,求直线
,求直线![]() 的斜率.
的斜率.
参考答案:
【答案】(1)![]() ;圆心为
;圆心为![]() ,半径为
,半径为![]() ;;(2)
;;(2)![]() 或
或![]() .
.
【解析】
试题分析:(1)直接由极坐标与直角坐标互化公式即可得出圆![]() 的直角坐标方程并求出其圆心的坐标与半径;(2)由(1)可知直线
的直角坐标方程并求出其圆心的坐标与半径;(2)由(1)可知直线![]() 的参数方程知直线过定点
的参数方程知直线过定点![]() ,然后由已知条件即可得出方程
,然后由已知条件即可得出方程 即可得出所求的结果.
即可得出所求的结果.
试题解析:(1)由![]() ,得
,得![]() .
.
将![]() ,代入可得
,代入可得![]() ,配方,得
,配方,得![]() ,所以圆心为
,所以圆心为![]() ,半径为
,半径为![]() .
.
(2)由直线![]() 的参数方程知直线过定点
的参数方程知直线过定点![]() ,
,
则由题意,知直线![]() 的斜率一定存在,因此不妨设直线
的斜率一定存在,因此不妨设直线![]() 的方程为
的方程为![]() 的方程为
的方程为![]() .
.
因为![]() ,所以
,所以 ,解得
,解得![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在边长为1的正方形
 内任取一点
内任取一点 ,求事件“
,求事件“ ”的概率;(2)某班在一次数学活动中,老师让全班56名同学每人随机写下一对都小于1的正实数
”的概率;(2)某班在一次数学活动中,老师让全班56名同学每人随机写下一对都小于1的正实数 、
、 ,统计出两数能与1构成锐角三角形的三边长的数对
,统计出两数能与1构成锐角三角形的三边长的数对 共有12对,请据此估计
共有12对,请据此估计 的近似值(精确到
的近似值(精确到 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】某制造厂商10月份生产了一批乒乓球,从中随机抽取
 个进行检查,测得每个球的直径(单位:
个进行检查,测得每个球的直径(单位: ),将数据进行分组,得到如下频率分布表:
),将数据进行分组,得到如下频率分布表:
(1)求
 、
、 、
、 及
及 、
、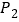 的值,并画出频率分布直方图(结果保留两位小数);
的值,并画出频率分布直方图(结果保留两位小数);(2)已知标准乒乓球的直径为
 ,直径误差不超过
,直径误差不超过 的为五星乒乓球,若这批乒乓球共有
的为五星乒乓球,若这批乒乓球共有 个,试估计其中五星乒乓球的数目;
个,试估计其中五星乒乓球的数目;(3)统计方法中,同一组数据常用该组区间的中点值(例如区间
 的中点值是
的中点值是 )作为代表,估计这批乒乓球直径的平均值和中位数.
)作为代表,估计这批乒乓球直径的平均值和中位数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了了解全校学生的上网情况,在全校采用随机抽样的方法抽取了40名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为5组:
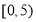 ,
,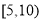 ,
,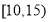 ,
,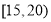 ,
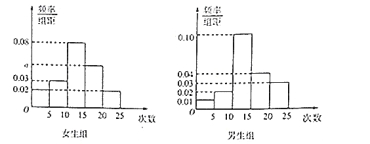
,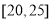 ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:(1)写出
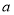 的值;
的值;(2)求抽取的40名学生中月上网次数不少于15次的学生人数;
(Ⅲ)在抽取的40名学生中,从月上网次数不少于20次的学生中随机抽取2人 ,求至少抽到1名女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两地相距为
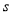 千米,汽车从甲地匀速行驶到乙地,速度每小时不超过
千米,汽车从甲地匀速行驶到乙地,速度每小时不超过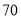 千米.已知汽车每小时的运输成本(单位:元)由可变部分和固定部分组成:固定部分为
千米.已知汽车每小时的运输成本(单位:元)由可变部分和固定部分组成:固定部分为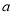 元,可变部分与速度
元,可变部分与速度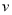 (单位;
(单位; 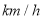 )的平方成正比,且比例系数为
)的平方成正比,且比例系数为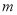 .
.(1)求汽车全程的运输成本
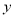 (单位:元)关于速度
(单位:元)关于速度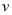 (单位;
(单位; 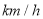 )的函数解析式;
)的函数解析式;(2)为了全程的运输成本最小,汽车应该以多大的速度行驶?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,且
,且 .
.(1)若函数
 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;(2)设函数
 ,当
,当 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】圆台的底面内的任意一条直径与另一个底面的位置关系是 ( )
A.平行B.相交C.在平面内D.不确定
相关试题

