【题目】圆过点![]() ,求
,求
(1)周长最小的圆的方程;
(2)圆心在直线![]() 上的圆的方程.
上的圆的方程.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)当周长最小时![]() 为圆的直径,由此可得所求圆的圆心和半径,即可得圆的方程;(2)线段
为圆的直径,由此可得所求圆的圆心和半径,即可得圆的方程;(2)线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 的交点
的交点![]() 即为圆心坐标,
即为圆心坐标, ![]() 即为半径,可得圆的方程.
即为半径,可得圆的方程.
解:(1)当AB为直径时,过A、B的圆的半径最小,从而周长最小.即AB中点(0,1)为圆心,半径r=![]() |AB|=
|AB|=![]() .则圆的方程为:x2+(y-1)2=10.
.则圆的方程为:x2+(y-1)2=10.
(2) 解法1:AB的斜率为k=-3,则AB的垂直平分线的方程是y-1=![]() x.即x-3y+3=0
x.即x-3y+3=0
由圆心在直线![]() 上得两直线交点为圆心即圆心坐标是C(3,2).
上得两直线交点为圆心即圆心坐标是C(3,2).
r=|AC|=![]() =2.∴圆的方程是(x-3)2+(y-2)2=20.
=2.∴圆的方程是(x-3)2+(y-2)2=20.
解法2:待定系数法
设圆的方程为:(x-a)2+(y-b)2=r2.
则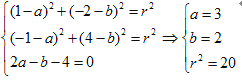
∴圆的方程为:(x-3)2+(y-2)2=20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)讨论函数
 的单调性;
的单调性;(2)若
 ,设
,设
 ,若对任意
,若对任意
 ,
, 恒成立,求实数
恒成立,求实数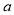 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种植物生长发育的数量y与时间x的关系如下表:
x
1
2
3
…
y
1
3
8
…
则下面的函数关系式中,能表达这种关系的是( )
A.y=2x-1 B.y=x2-1
C.y=2x-1 D.y=1.5x2-2.5x+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 :方程
:方程 有两个不等的负根;
有两个不等的负根;  :方程
:方程 无实根.若“
无实根.若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,求
”为假,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日 期
12月1日
12月2日
12月3日
12月4日
12月5日
温差x(°C)
10
11
13
12
8
发芽数y(颗)
23
25
30
26
16
(1)请根据12月2日至12月4日的数据,求出y关于x的线性回归方程
 (其中已计算出
(其中已计算出 );
);(2)若由线性回归方程得到的估计数据与所选出的检验数据(选取的检验数据是12月1日与12月5日的两组数据)的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1-i)2·i等于
A.2-2iB. 2+2iC.-2 D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的
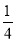 ,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:
,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
相关试题

