(本题满分12分)
已知二次函数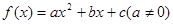 的图象过点
的图象过点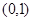 ,且与
,且与 轴有唯一的交点
轴有唯一的交点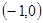 .(1)求
.(1)求 的表达式;
的表达式;
(2)当 时,求函数
时,求函数 的最小值。
的最小值。
(1) 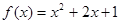 (2) 当
(2) 当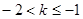 时,最小值为
时,最小值为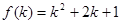 ,
,
当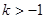 时,最小值为
时,最小值为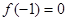 .
.
解析试题分析:(1)依题意得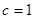 ,
,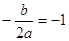 ,
,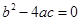 , ……3分
, ……3分
解得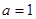 ,
,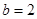 ,
,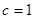 ,从而
,从而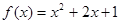 ; ……6分
; ……6分
(2) 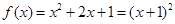 ,函数的图象为开口向上、对称轴为
,函数的图象为开口向上、对称轴为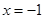 的抛物线,
的抛物线,
结合图象可知,当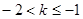 时,函数单调递减,
时,函数单调递减,
所以最小值为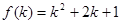 , ……8分
, ……8分
当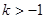 时,函数在
时,函数在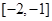 上单调递减,在
上单调递减,在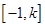 上单调递增,
上单调递增,
所以最小值为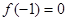 . ……12分
. ……12分
考点:本小题主要考查二次函数解析式的求法和二次函数最值问题,考查学生分类讨论和数形结合等数学思想的应用和运算求解能力.
点评:求闭区间上二次函数的值域时,要结合函数的图象进行求解,不要出现简单的把端点代入求解的错误.

