(本小题满分12分) 已知函数f(x)=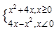 (1)作出函数
(1)作出函数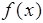 的图像简图,并指出函数
的图像简图,并指出函数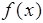 的单调区间;
(2)若f(2-a2)>f(a),求实数a的取值范围.
的单调区间;
(2)若f(2-a2)>f(a),求实数a的取值范围.
解析:(1) f(x)在(-∞,+∞)上是单调递增函数;(2)-2<a<1.
【解析】本试题主要是考查了分段函数的作图,以及函数的单调性和不等式的求解综合运用。
(1)利用作出两端二次函数的图像得到第一问。
(2)由(1)可知f(x)在(-∞,+∞)上是单调递增函数
故由f(2-a2)>f(a)得2-a2>a,求解得到参数a的范围。
解析:(1) 略 ……………………………………………4分
由f(x)的图象可知f(x)在(-∞,+∞)上是单调递增函数,……………………7分
(2)由(1)可知f(x)在(-∞,+∞)上是单调递增函数
故由f(2-a2)>f(a)得2-a2>a,即a2+a-2<0,…………………………………10分
解得-2<a<1.…………………………………………12分
20. 【题文】 (本小题满分13分)
(1)证明:函数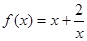 在
在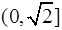 上是减函数,在[
上是减函数,在[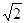 ,+∞)上是增函数;
,+∞)上是增函数;
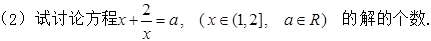
【答案】解: (1)证明:见解析;
(2)当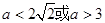 时,方程无解;当
时,方程无解;当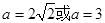 方程有一个解;当
方程有一个解;当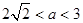 时,方程有两个解.
时,方程有两个解.
【解析】本试题主要是考查了二次函数的单调性以及函数与方程的综合运用。
(1)根据但单调性的定义法,设变量,作差,变形定号,下结论。
(2)在第一问的基础上,结合单调性,得到函数的最值,然后分析得到参数的范围。
解: (1)证明:设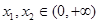 ,且
,且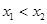
则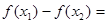
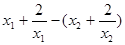 =
= =
=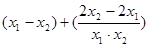
=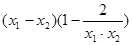 =
=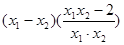 .………4分
.………4分
(ⅰ)若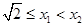 ,
,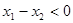 且
且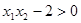 ,
,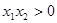 ,所以
,所以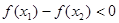 ,
,
即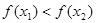 .所以函数
.所以函数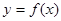 在区间[
在区间[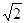 ,+∞)上单调递增.………6分
,+∞)上单调递增.………6分
(ⅱ)若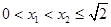 ,则
,则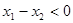 且
且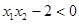 ,
,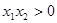 ,
,
所以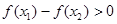 ,即
,即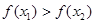 .所以函数
.所以函数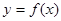 在区间[
在区间[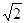 ,+∞)上单调递减.………………………………8分
,+∞)上单调递减.………………………………8分
(2)由(1)知函数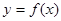 在区间(1,
在区间(1,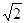 )上单调递减,在区间[
)上单调递减,在区间[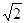 ,2]上单调递增
,2]上单调递增
所以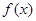 的最小值=
的最小值=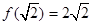 ,
,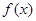 的最大值=
的最大值=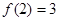 ……………………10分
……………………10分
故当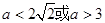 时,方程无解;当
时,方程无解;当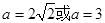 方程有一个解;当
方程有一个解;当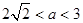 时,方程有两个解.………………………………………13分
时,方程有两个解.………………………………………13分

