【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差 x (℃) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是:先用2、3、4、5月的4组数据求线性回归方程,再用1月和6月的2组数据进行检验.
(1)请根据2、3、4、5月的数据,求出y关于x的线性回归方程![]()
![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考公式:  ,
, ![]()
 )
)
参考数据:11×25+13×29+12×26+8×16=![]() 1092,112+132+122+82=498.
1092,112+132+122+82=498.
参考答案:
【答案】(1)![]()
![]() (2)线性回归方程是理想的.
(2)线性回归方程是理想的.
【解析】试题分析:(1)根据给出的公式计算回归方程.(2)根据(1)中的回归方程计算预测值,看它与实际值的差是否不超过2即可.
解析:(1)由数据求得![]()
![]() ,由公式求得
,由公式求得![]() ,再由
,再由![]() ,所以
,所以![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
. ![]()
(2)当![]() 时,
时, ![]()
![]() ,
, ![]()
![]() ;同样,当
;同样,当![]() 时,
时, ![]()
![]() ,
, ![]() ,所以,该小组所得线性回归方程是理想的.
,所以,该小组所得线性回归方程是理想的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知事件“在矩形ABCD的边CD上随机取一点P,使△APB的最大边是AB”发生的概率为
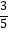 ,则
,则 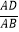 =( )
=( )
A.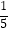
B.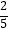
C.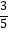
D.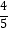
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=2AD=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,构成四棱锥A1﹣BCDE,若M为线段A1C的中点,在翻转过程中有如下4个命题: ①MB∥平面A1DE;
②存在某个位置,使DE⊥A1C;
③存在某个位置,使A1D⊥CE;
④点A1在半径为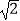 的圆面上运动,
的圆面上运动,
其中正确的命题个数是( )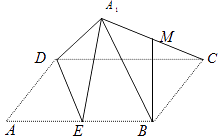
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}为等差数列,公差为d,且0<d<1,a5≠
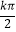 (k∈Z),sin2a3+2sina5cosa5=sin2a7 , 函数f(x)=dsin(wx+4d)(w>0)满足:在
(k∈Z),sin2a3+2sina5cosa5=sin2a7 , 函数f(x)=dsin(wx+4d)(w>0)满足:在 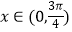 上单调且存在
上单调且存在 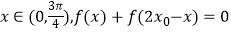 ,则w范围是 .
,则w范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】遂宁市观音湖港口船舶停靠的方案是先到先停.
(1)若甲乙两艘船同时到达港口,双方约定各派一名代表从1,2,3,4,5中各随机选一个数(甲、乙选取的数互不影响),若两数之和为偶数,则甲先停靠;若两数之和为奇数,则乙先停靠,这种规则是否公平?请说明理由.
(2)根据以往经验,甲船将于早上7:00~8:00到达,乙船将于早上7:30~8:30到达,请求出甲船先停靠的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆心在
 轴上的圆
轴上的圆 与直线
与直线 切于点
切于点 .
.(1)求圆
 的标准方程;
的标准方程;(2)已知
 ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线 与圆
与圆 交于
交于 两点.
两点.(ⅰ)求证:
 为定值;
为定值;(ⅱ)求
 的最大值.
的最大值.
相关试题

