

【题目】已知数列![]() ,
,![]() ,
,![]() 满足:
满足:![]() ,
,![]() .
.
(1)若![]() 是等差数列,且公差
是等差数列,且公差![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]() ;
;
(2)若![]() 、
、![]() 均是等差数列,且数列
均是等差数列,且数列![]() 的公差
的公差![]() ,
,![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)![]() 是等差数列,且公差
是等差数列,且公差![]() ,
,![]() ,所以
,所以![]() ,由
,由![]() ,进而算出
,进而算出![]() ,利用累加法,即可求出数列
,利用累加法,即可求出数列![]() 的通项公式
的通项公式![]() ;
;
(2)因为![]() 是等差数列,且数列
是等差数列,且数列![]() 的公差
的公差![]() ,
,![]() ,所以
,所以![]() ,得出
,得出![]() ,根据题意,进而求出
,根据题意,进而求出![]() ,可得出
,可得出![]() 的首项和公差,求得
的首项和公差,求得![]() ,所以
,所以![]() ,分类讨论
,分类讨论![]() 为奇数和偶数时,求出数列
为奇数和偶数时,求出数列![]() 的通项公式.
的通项公式.
(1)因为![]() 是等差数列,且公差
是等差数列,且公差![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
因为![]() ,
,
即:![]() ,
,
所以![]() ,
,
![]() ,
,
…
![]() ,
,![]() ,
,
上面![]() 式子相加得:
式子相加得:
![]() ,
,
所以![]() ,
,
当![]() 时也满足上面
时也满足上面![]() 的通项,
的通项,
综上:数列![]() 的通项公式
的通项公式![]() ,
,
(2)因为![]() 是等差数列,且数列
是等差数列,且数列![]() 的公差
的公差![]() ,
,![]() ,
,
所以![]() ①,
①,
![]() ②,
②,
![]() 得:
得:![]() ,即
,即![]() ,
,
所以![]() ,
,![]() ,
,
因为![]() 是等差数列,设等差数列
是等差数列,设等差数列![]() 的公差为
的公差为![]() ,
,
所以![]() ,
,![]() ,由此解得:
,由此解得:![]() ,
,![]() ,
,
所以![]() ,满足
,满足![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
①当![]() 时,
时,![]() ,所以
,所以![]() ,
,
②当![]() 时,
时,![]() ,所以
,所以![]() ,
,
综上:数列![]() 的通项公式
的通项公式![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4-5:不等式选讲
已知函数f(x)=log2(|x+1|+|x﹣2|﹣m).
(1)当m=7时,求函数f(x)的定义域;
(2)若关于x的不等式f(x)≥2的解集是R,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请全校
的值:先请全校![]() 名同学每人随机写下一个都小于
名同学每人随机写下一个都小于![]() 的正实数对
的正实数对![]() ;再统计两数能与
;再统计两数能与![]() 构成钝角三角形三边的数对
构成钝角三角形三边的数对![]() 的个数
的个数![]() ;最后再根据统计数
;最后再根据统计数![]() 估计
估计![]() 的值,那么可以估计
的值,那么可以估计![]() 的值约为( )
的值约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,以坐标原点
为参数,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,曲线
轴的正半轴为极轴,取相同长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)设射线![]() 与曲线
与曲线![]() 交于不同于极点的点
交于不同于极点的点![]() ,与曲线
,与曲线![]() 交于不同于极点的点
交于不同于极点的点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济实力的不断提升,居民收人也在不断增加。某家庭2018年全年的收入与2014年全年的收入相比增加了一倍,实现翻番.同时该家庭的消费结构随之也发生了变化,现统计了该家庭这两年不同品类的消费额占全年总收入的比例,得到了如下折线图:
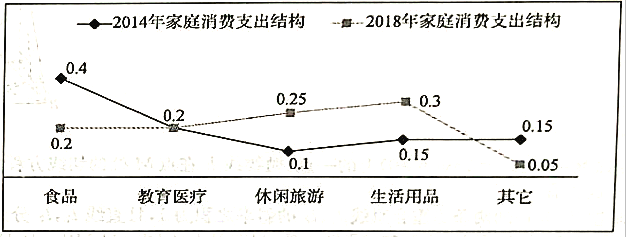
则下列结论中正确的是( )
A. 该家庭2018年食品的消费额是2014年食品的消费额的一半
B. 该家庭2018年教育医疗的消费额与2014年教育医疗的消费额相当
C. 该家庭2018年休闲旅游的消费额是2014年休闲旅游的消费额的五倍
D. 该家庭2018年生活用品的消费额是2014年生活用品的消费额的两倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某客户考察了一款热销的净水器,使用寿命为十年,改款净水器为三级过滤,每一级过滤都由核心部件滤芯来实现.在使用过程中,一级滤芯需要不定期更换,其中每更换![]() 个一级滤芯就需要更换
个一级滤芯就需要更换![]() 个二级滤芯,三级滤芯无需更换.其中一级滤芯每个
个二级滤芯,三级滤芯无需更换.其中一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元.记一台净水器在使用期内需要更换的二级滤芯的个数构成的集合为
元.记一台净水器在使用期内需要更换的二级滤芯的个数构成的集合为![]() .如图是根据
.如图是根据![]() 台该款净水器在十年使用期内更换的一级滤芯的个数制成的柱状图.
台该款净水器在十年使用期内更换的一级滤芯的个数制成的柱状图.
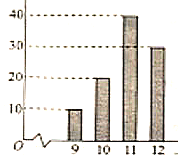
(1)结合图,写出集合![]() ;
;
(2)根据以上信息,求出一台净水器在使用期内更换二级滤芯的费用大于![]() 元的概率(以
元的概率(以![]() 台净水器更换二级滤芯的频率代替
台净水器更换二级滤芯的频率代替![]() 台净水器更换二级滤芯发生的概率);
台净水器更换二级滤芯发生的概率);
(3)若在购买净水器的同时购买滤芯,则滤芯可享受![]() 折优惠(使用过程中如需再购买无优惠).假设上述
折优惠(使用过程中如需再购买无优惠).假设上述![]() 台净水器在购机的同时,每台均购买
台净水器在购机的同时,每台均购买![]() 个一级滤芯、
个一级滤芯、![]() 个二级滤芯作为备用滤芯(其中
个二级滤芯作为备用滤芯(其中![]() ,
,![]() ),计算这
),计算这![]() 台净水器在使用期内购买滤芯所需总费用的平均数.并以此作为决策依据,如果客户购买净水器的同时购买备用滤芯的总数也为
台净水器在使用期内购买滤芯所需总费用的平均数.并以此作为决策依据,如果客户购买净水器的同时购买备用滤芯的总数也为![]() 个,则其中一级滤芯和二级滤芯的个数应分别是多少?
个,则其中一级滤芯和二级滤芯的个数应分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校需要从甲、乙两名学生中选一人参加数学竞赛,抽取了近期两人![]() 次数学考试的成绩,统计结果如下表:
次数学考试的成绩,统计结果如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩(分) |
|
|
|
|
|
乙的成绩(分) |
|
|
|
|
|
(1)若从甲、乙两人中选出一人参加数学竞赛,你认为选谁合适?请说明理由.
(2)若数学竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若答对,则可参加复赛,否则被淘汰.
道,若答对,则可参加复赛,否则被淘汰.
方案二:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若至少答对其中
道,若至少答对其中![]() 道,则可参加复赛,否则被润汰.
道,则可参加复赛,否则被润汰.
已知学生甲、乙都只会![]() 道备选题中的
道备选题中的![]() 道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆右焦点
,过椭圆右焦点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当直线![]() 与
与![]() 轴不垂直时,在
轴不垂直时,在![]() 轴上是否存在一点
轴上是否存在一点![]() (异于点
(异于点![]() ),使
),使![]() 轴上任意点到直线
轴上任意点到直线![]() ,
,![]() 的距离均相等?若存在,求
的距离均相等?若存在,求![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com