【题目】已知数列{an}是公差为2的等差数列,数列{bn满足bn+1﹣bn=an , 且b2=﹣18,b3=﹣24.
(1)求数列{an}的通项公式;
(2)求bn取得最小值时n的值.
参考答案:
【答案】
(1)解:由题意知d=2,
再由bn+1﹣bn=an,且b2=﹣18,b3=﹣24,得a2=b3﹣b2=﹣6,
则a1=a2﹣d=﹣6﹣2=﹣8,
∴an=﹣8+2(n﹣1)=2n﹣10;
(2)解:bn+1﹣bn=2n﹣10,
∴b2﹣b1=2×1﹣10,
b3﹣b2=2×2﹣10,
…
bn﹣bn﹣1=2(n﹣1)﹣10(n≥2),
累加得:bn=b1+2[1+2+…+(n﹣1)]﹣10(n﹣1)
=b2﹣a1+2[1+2+…+(n﹣1)]﹣10(n﹣1),
=﹣10+ ![]() =
= ![]() .
.
∴当n=5或6时,bn取得最小值为b5=b6=﹣30
【解析】(1)由已知求得a2 , 结合公差求得首项,则数列{an}的通项公式可求;(2)把数列{an}的通项公式代入bn+1﹣bn=an , 利用累加法求得bn , 结合二次函数求得bn取得最小值时n的值.
【考点精析】根据题目的已知条件,利用数列的通项公式的相关知识可以得到问题的答案,需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
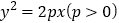 的焦点为
的焦点为 ,准线为
,准线为 ,过点
,过点 的直线交拋物线于
的直线交拋物线于 ,
, 两点,过点
两点,过点 作准线
作准线 的垂线,垂足为
的垂线,垂足为 ,当
,当 点坐标为
点坐标为 时,
时, 为正三角形,则此时
为正三角形,则此时 的面积为____________
的面积为____________ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的函数
上的函数 .
. 求函数
求函数 的单调减区间;
的单调减区间; Ⅱ
Ⅱ 若关于
若关于 的方程
的方程 有两个不同的解,求实数
有两个不同的解,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】求满足下列条件的椭圆或双曲线的标准方程:
(1)椭圆的焦点在
 轴上,焦距为4,且经过点
轴上,焦距为4,且经过点 ;
;(2)双曲线的焦点在
 轴上,右焦点为
轴上,右焦点为 ,过
,过 作重直于
作重直于 轴的直线交双曲线于
轴的直线交双曲线于 ,
, 两点,且
两点,且 ,离心率为
,离心率为 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=cos(2x﹣
 )﹣cos2x.
)﹣cos2x.
(1)求f( )的值;
)的值;
(2)求函数f(x)的最小正周期和单调递增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 过点
过点 ,圆
,圆 :
: .
.(1)当直线
 与圆相切时,求直线
与圆相切时,求直线 的一般方程;
的一般方程;(2)若直线与圆相交,且弦长为
 ,求直线
,求直线 的一般方程.
的一般方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
求分数在[120,130)内的频率,并补全这个频
率分布直方图;
统计方法中,同一组数据常用该组区间的中点
值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段[120,130)内的概率.

相关试题

