练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知倾斜角为的直线经过抛物线的焦点，与抛物线相交于、两点，且.

    （1）求抛物线的方程；

    （2）设为抛物线上任意一点（异于顶点），过做倾斜角互补的两条直线、，交抛物线于另两点、，记抛物线在点的切线的倾斜角为，直线的倾斜角为，求证：与互补.

    【答案】（1）（2）证明见解析

    【解析】

    （1）根据题意，设直线方程为，联立方程，根据抛物线的定义即可得到结论；

    （2）根据题意，设的方程为，联立方程得，同理可得，进而得到，再利用点差法得直线的斜率，利用切线与导数的关系得直线的斜率，进而可得与互补.

    （1）由题意设直线的方程为，令、，

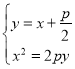    联立，得

    ，

    根据抛物线的定义得，

    又，

    故所求抛物线方程为.

    （2）依题意，设，，

    设的方程为，与联立消去得，

    ，同理

    ，直线的斜率=

    切线的斜率，

    由，即与互补.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】有一块半圆形的空地，直径米，政府计划在空地上建一个形状为等腰梯形的花圃，如图所示，其中为圆心，，在半圆上，其余为绿化部分，设.

    （1）记花圃的面积为，求的最大值；

    （2）若花圃的造价为10元/米，在花圃的边、处铺设具有美化效果的灌溉管道，铺设费用为500元/米，两腰、不铺设，求满足什么条件时，会使总造价最大.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一次考试结束后，随机抽查了某校高三（1）班5名同学的数学与物理成绩如下表：

    学生

    数学

    89

    91

    93

    95

    97

    物理

    87

    89

    89

    92

    93

    （Ⅰ）分别求这5名同学数学与物理成绩的平均分与方差，并估计该班数学与物理成绩那科更稳定；

    （Ⅱ）从以上5名同学中选2人参加一项活动，求选中的学生中至少有一个物理成绩高于90分的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若曲线在处的切线与轴平行，求；

    （2）已知在上的最大值不小于，求的取值范围；

    （3）写出所有可能的零点个数及相应的的取值范围.（请直接写出结论）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在等腰直角中，，，点、分别是、的中点.现沿边折起成如图四棱锥，为中点.

    （1）证明：面；

    （2）当时，求二面角的平面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知空间中两条直线，所成的角为，为空间中给定的一个定点，直线过点且与直线和直线所成的角都是，则下列选项正确的是（ ）

    A.当时，满足题意的直线不存在

    B.当时，满足题意的直线有且仅有1条

    C.当时，满足题意的直线有且仅有2条

    D.当时，满足题意的直线有且仅有3条

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知甲盒内有大小相同的1个红球和3个黑球，乙盒内有大小相同的3个红球和3个黑球，现从甲、乙两个盒内各任取2个球。

    （1）求取出的4个球中没有红球的概率；

    （2）求取出的4个球中恰有1个红球的概率；

    （3）设为取出的4个球中红球的个数，求的分布列和数学期望。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四个命题：

    ①在回归分析中， 可以用来刻画回归效果， 的值越大，模型的拟合效果越好；

    ②在独立性检验中，随机变量的值越大，说明两个分类变量有关系的可能性越大；

    ③在回归方程中，当解释变量每增加1个单位时，预报变量平均增加1个单位；

    ④两个随机变量相关性越弱，则相关系数的绝对值越接近于1；

    其中真命题是：

    A. ①④ B. ②④ C. ①② D. ②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，().

    （1）若曲线在点处的切线方程为，求实数am的值；

    （2）关于x的方程能否有三个不同的实根？证明你的结论；

    （3）若对任意恒成立，求实数a的取值范围.

    查看答案和解析>>

    同步练习册答案