(本小题满分12分)
已知函数f(x)=alnx,(a∈R)g(x)=x2,记F(x)=g(x)-f(x)
(Ⅰ)判断F(x)的单调性;
(Ⅱ)当a≥时,若x≥1,求证:g(x-1)≥f();
(Ⅲ)若F(x)的极值为,问是否存在实数k,使方程g(x)-f(1+x2)=k有四个不同实数根?若存在,求出实数k的取值范围;若不存在,请说明理由。
【答案】
解:(Ⅰ)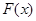 的定义域为(0,+∞),
的定义域为(0,+∞), 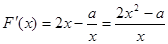
当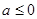 时,
时,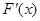 >0恒成立
∴
>0恒成立
∴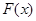 在(0,+∞)上单调递增;
在(0,+∞)上单调递增;
当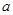 >0时,若
>0时,若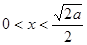 ,
,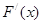 <0 ∴
<0 ∴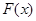 在(0,
在(0,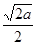 )上单调递减;
)上单调递减;
若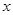 >
>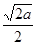 ,
,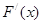 >0,∴
>0,∴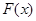 在(
在(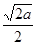 ,+∞)上单调递增.............4分
,+∞)上单调递增.............4分
(Ⅱ)令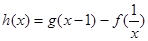 ,则
,则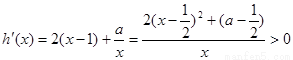 ,
,
所以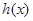 在[1,+∞)上单调递增,∴
在[1,+∞)上单调递增,∴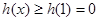 ,∴
,∴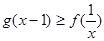 ...8分
...8分
(Ⅲ)由(1)知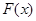 仅当
仅当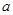 >0时,在
>0时,在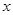 =
=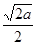 处取得极值
处取得极值
由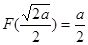 可得
可得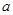 =2 ∴
=2 ∴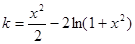 ...1
...1
令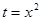 ,得
,得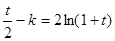 ...2
...2
方程1有四个不同的根,则方程2有两个不同的正根,
令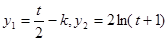 ,当直线
,当直线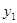 与曲线
与曲线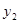 相切时,由导数知识可得切点坐标(3,
相切时,由导数知识可得切点坐标(3,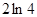 ) ∴切线方程为
) ∴切线方程为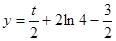 ,其在y轴上截距为
,其在y轴上截距为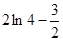 ;
;
当直线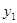 在y轴上截距
在y轴上截距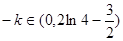 时,
时,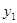 和
和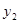 在y轴右侧有两个不同交点,所以k的取值范围为(
在y轴右侧有两个不同交点,所以k的取值范围为(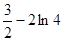 ,0)......................................12分
,0)......................................12分
(附:也可用导数求解)
【解析】略

