【题目】关于函数，，下列说法正确的是（ ）

A.当时，在处的切线方程为

B.当时，存在唯一极小值点，且

C.对任意，在上均存在零点

D.存在，在上有且只有一个零点

【答案】ABD

【解析】

当时，，求出，得到在处的切线的点斜式方程，即可判断选项A；求出的解，确定单调区间，进而求出极值点个数，以及极值范围，可判断选项B；令，当时，分离参数可得，设，求出的极值最值，即可判断选项C，D的真假.

当时，，

,

所以在处的切线方程为，

即，所以选项A正确；

当时，，

当时，，

当时，单调递增，

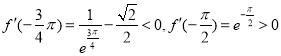
所以存在，使得，

当，

所以是唯一极小值点，且，

，

，

，所以选项B正确；

令，当时，，

设，

，

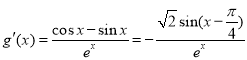令，

由图像可知，

当时取极大值，又，

，

当时极小值，又，

，

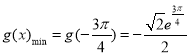所以当，，

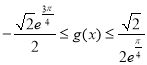当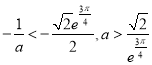时，

与直线没有交点，

即在上不存在零点，所以选项C错误；

当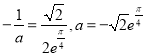时，与直线有唯一交点，

此时在上有且只有一个零点，所以选项D正确.

故选：ABD.

关闭