【题目】椭圆规是用来画椭圆的一种器械，它的构造如图所示，在一个十字形的金属板上有两条互相垂直的导槽，在直尺上有两个固定的滑块A，B，它们可分别在纵槽和横槽中滑动，在直尺上的点M处用套管装上铅笔，使直尺转动一周，则点M的轨迹C是一个椭圆，其中|MA|＝2，|MB|＝1，如图，以两条导槽的交点为原点O，横槽所在直线为x轴，建立直角坐标系.

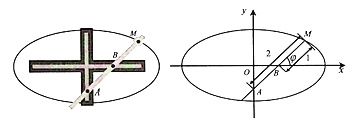
（1）将以射线Bx为始边，射线BM为终边的角xBM记为φ（0≤φ＜2π），用表示点M的坐标，并求出C的普通方程；

（2）已知过C的左焦点F，且倾斜角为α（0≤α）的直线l1与C交于D，E两点，过点F且垂直于l1的直线l2与C交于G，H两点.当，|GH|，依次成等差数列时，求直线l2的普通方程.

【答案】（1），；（2）

【解析】

（1）用三角函数表示出点M的坐标，直接利用转换关系把极坐标方程转换为直角坐标方程；（2）设出直线l1的参数方程，与椭圆方程联立利用直线参数的几何意义求出、，根据题意有，列出方程求出直线l1的斜率即可求得直线l2的方程.

（1）设M（x，y）依题意得：x＝2cosφ，y＝sinφ，

所以M（2cosφ，sinφ），

由于cos2φ+sin2φ＝1，整理得.

（2）由于直线l1的倾斜角为α（），且l1⊥l2，

所以直线l2的倾斜角为，依题意易知：F（），

可设直线l1的方程为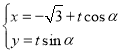（t为参数），

代入得到：，

易知，

设点D和点E对应的参数为t1和t2，

所以，.

则，

由参数的几何意义：，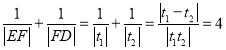

设G、H对应的参数为t3和t4，同理对于直线l2，将α换为，

所以，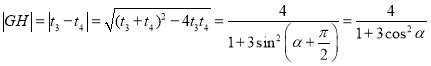

由于，|GH|，依次成等差数列，

所以，则，解得，

所以，又，所以，

所以直线l2的斜率为，直线l2的直角坐标方程为x.

关闭