【题目】已知函数 ,若方程
,若方程![]() 有三个不同解,则实数
有三个不同解,则实数![]() 的取值范围是___________。
的取值范围是___________。
【答案】![]() .
.
【解析】
画出函数f(x)的图象,求出![]() 与
与![]() 有三个不同的交点时的临界值,从而求出a的范围即可.
有三个不同的交点时的临界值,从而求出a的范围即可.
由题意知方程![]() 有三个不同解,
有三个不同解,
即![]() 与
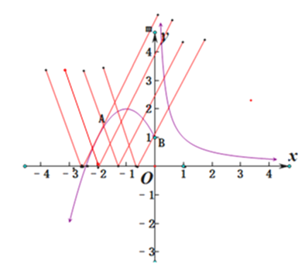
与![]() 有三个不同的交点,作出f(x)的图象,
有三个不同的交点,作出f(x)的图象,
当f′(x)=-2x-2,当f′(x)=-2x-2=-2时,解得x=0,
即y=-2x+a与f(x)切于B,不满足题意;
如图:再将![]() 从右向左平移,当
从右向左平移,当![]() 过B(0,1)时,
过B(0,1)时,
满足条件,此时(0,1)在y=2x-a上,解得a=-1;
将![]() 向左平移至与
向左平移至与![]() 相切时,此时直线m与f(x)切于A,不满足条件,
相切时,此时直线m与f(x)切于A,不满足条件,
又f′(x)=-2x-2=2,则x=-2,即A(-2,1)在y=2x-a上,解得a=-5,
所以![]() 时满足题意,
时满足题意,
故答案为![]() .
.