【题目】已知圆![]() 经过
经过![]() ,
,![]() ,
,![]() 三点.
三点.
(1)求圆![]() 的标准方程;
的标准方程;
(2)若过点N ![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦AB的长为
截得的弦AB的长为![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
参考答案:
【答案】(1) ![]() (2) 30°或90°.
(2) 30°或90°.
【解析】
(1)解法一:将圆的方程设为一般式,将题干三个点代入圆的方程,解出相应的参数值,即可得出圆![]() 的一般方程,再化为标准方程;
的一般方程,再化为标准方程;
解法二:求出线段![]() 和
和![]() 的中垂线方程,将两中垂线方程联立求出交点坐标,即为圆心坐标,然后计算
的中垂线方程,将两中垂线方程联立求出交点坐标,即为圆心坐标,然后计算![]() 为圆的半径,即可写出圆
为圆的半径,即可写出圆![]() 的标准方程;
的标准方程;
(2)先利用勾股定理计算出圆心到直线![]() 的距离为
的距离为![]() ,并对直线
,并对直线![]() 的斜率是否存在进行分类讨论:一是直线
的斜率是否存在进行分类讨论:一是直线![]() 的斜率不存在,得出直线
的斜率不存在,得出直线![]() 的方程为
的方程为![]() ,验算圆心到该直线的距离为
,验算圆心到该直线的距离为![]() ;
;
二是当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,并表示为一般式,利用圆心到直线的距离为
,并表示为一般式,利用圆心到直线的距离为![]() 得出关于
得出关于![]() 的方程,求出
的方程,求出![]() 的值。结合前面两种情况求出直线
的值。结合前面两种情况求出直线![]() 的倾斜角。
的倾斜角。
(1)解法一:设圆![]() 的方程为
的方程为![]() ,
,
则 ∴
∴
即圆![]() 为
为![]() ,
,
∴圆![]() 的标准方程为
的标准方程为![]() ;
;
解法二:则![]() 中垂线为
中垂线为![]() ,
,![]() 中垂线为
中垂线为![]() ,
,
∴圆心![]() 满足
满足![]() ∴
∴![]() ,
,
半径![]() ,
,
∴圆![]() 的标准方程为
的标准方程为![]() .
.
(2)①当斜率不存在时,即直线![]() 到圆心的距离为1,也满足题意,
到圆心的距离为1,也满足题意,
此时直线![]() 的倾斜角为90°,
的倾斜角为90°,
②当斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
由弦长为4,可得圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
![]() ,
,
∴![]() ,此时直线
,此时直线![]() 的倾斜角为30°,
的倾斜角为30°,
综上所述,直线![]() 的倾斜角为30°或90°.
的倾斜角为30°或90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照[0,2],(2,4],…,(14,16]分成8组,制成了如图1所示的频率分布直方图.

(Ⅰ)假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况.
( i)现从全市居民中依次随机抽取5户,求这5户居民恰好3户居民的月用水用量都超过12吨的概率;
(ⅱ)试估计全市居民用水价格的期望(精确到0.01);
(Ⅱ)如图2是该市居民李某2016年1~6月份的月用水费y(元)与月份x的散点图,其拟合的线性回归方程是 .若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车公司对最近6个月内的市场占有率进行了统计,结果如表;
月份代码
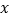
1
2
3
4
5
6
市场占有率
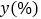
11
13
16
15
20
21
(1)可用线性回归模型拟合
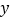 与
与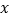 之间的关系吗?如果能,请求出
之间的关系吗?如果能,请求出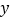 关于
关于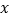 的线性回归方程,如果不能,请说明理由;
的线性回归方程,如果不能,请说明理由;(2)公司决定再采购
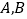 两款车扩大市场,
两款车扩大市场, 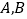 两款车各100辆的资料如表:
两款车各100辆的资料如表:车型
报废年限(年)
合计
成本
1
2
3
4
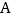
10
30
40
20
100
1000元/辆
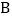
15
40
35
10
100
800元/辆
平均每辆车每年可为公司带来收入
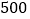 元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?
元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?参考数据:
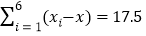 ,
,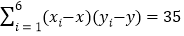 ,
,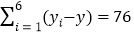 ,
,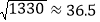 .
.参考公式:相关系数
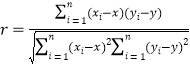 ;
;回归直线方程为
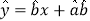 ,其中
,其中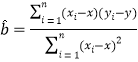 ,
,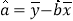 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
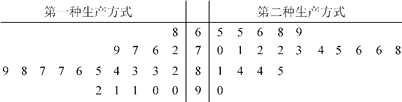
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数
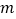 ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过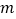 和不超过
和不超过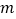 的工人数填入下面的列联表:
的工人数填入下面的列联表:超过
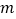
不超过
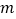
第一种生产方式
第二种生产方式
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:
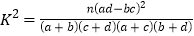 ,
, 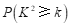
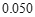
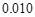
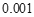
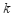
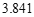

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的右焦点F(1,0),椭圆Γ的左,右顶点分别为M,N.过点F的直线l与椭圆交于C,D两点,且△MCD的面积是△NCD的面积的3倍.
的右焦点F(1,0),椭圆Γ的左,右顶点分别为M,N.过点F的直线l与椭圆交于C,D两点,且△MCD的面积是△NCD的面积的3倍.
(Ⅰ)求椭圆Γ的方程;
(Ⅱ)若CD与x轴垂直,A,B是椭圆Γ上位于直线CD两侧的动点,且满足∠ACD=∠BCD,试问直线AB的斜率是否为定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=e2x(ax2+2x﹣1),a∈R.
(Ⅰ)当a=4时,求证:过点P(1,0)有三条直线与曲线y=f(x)相切;
(Ⅱ)当x≤0时,f(x)+1≥0,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.若直线l的极坐标方程为
 ,曲线C的极坐标方程为:ρsin2θ=cosθ,将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1 .
,曲线C的极坐标方程为:ρsin2θ=cosθ,将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1 .
(Ⅰ)求曲线C1的直角坐标方程;
(Ⅱ)已知直线l与曲线C1交于A,B两点,点P(2,0),求|PA|+|PB|的值.
相关试题

